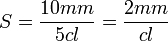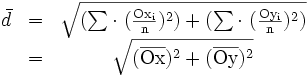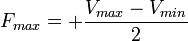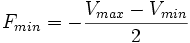Qualité métrologique des appareils de mesure - Définition
La qualité métrologique d'un appareil de mesure est l'ensemble des caractéristiques qui fera qu'un appareil de mesure effectuera les mesures avec la qualité correspondante à l'attente de l'utilisateur.
La qualité d'un appareil est définie par les caractéristiques suivantes :
-
- L'étendue
- la sensibilité
- la précision
- la justesse
- la fidélité
l'étendue de mesurage
C'est le domaine de variation possible de la grandeur à mesurer. Elle est définie par une valeur minimale et une valeur maximale.
Exemple :
Un voltmètre aura une étendue de mesure comprise entre 1 volt et 10 volts.
La sensibilité
La sensibilité d'un appareil est la plus petite variation de mesure qu'il peut déceler.
Cas général
La sensibilité est un paramètre exprimant la variation du signal de sortie d'un appareil de mesure en fonction de la variation du signal d'entrée.
Un appareil est d'autant plus sensible qu'une petite variation de la grandeur G à mesurer provoquera un changement plus grand de l'appareil de mesure.
Nota : si la valeur d'entrée est de même nature que la valeur de sortie, la sensibilité est appelée gain.
La sensibilité au voisinage d'une valeur donnée de la grandeur G à mesurer s'exprime de la manière suivante :
-
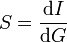
- I: Indication donnée par l'essai
- G: Quantité de grandeur à mesurer
On considère généralement qu'il s'agit de la pente de la courbe de graduation sur un intervalle : la sensibilité moyenne.
On peut écrire alors :
-
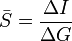
Exemple :
L'échelon d'un volucompteur est de 1 cm et la valeur d'échelon est de 5 cl.
Cas d'un appareil linéaire
La formule (lien) n'a de sens que si sur cet intervalle de mesure l'appareil est linéaire. C’est-à-dire si la sortie est proportionnelle à l'entrée.
-
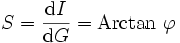
En pratique, on réalise une courbe d'étalonnage où la linéarité est approchée. Pour déterminer la droite on peut utiliser la méthode des moindres carrés.
Sensibilité et résolution
Ne pas confondre la sensibilité avec la résolution (ou pouvoir de résolution).
La résolution est le plus petit écart entre deux valeurs, tel que l'appareil en donne une mesure différente
Exemple :
Un voltmètre indique 100 volts. Une variation de 0,1 volt fait bouger l'aiguille du voltmètre alors qu'une variation de 0,05 volt ne fait pas bouger l'aiguille. La résolution du voltmètre est de 0.1 volt.
La précision
Un instrument de mesure est d'autant plus précis que les résultats de mesure qu'il indique coïncident avec la valeur vraie (par définition théorique) que l'on cherche à mesurer.
La précision est plus aisée à définir par l'erreur de précision. Elle s'exprime en unité de grandeur (erreur absolue) ou en pourcentage (erreur relative).
En dehors des conditions opératoires, la précision d'un appareil est essentiellement lié à deux types de caractéristiques : la justesse et la fidélité. Un appareils est précis s'il est à la fois juste et fidèle.
La précision d'appareil de mesure peut également être entachée par des causes extérieures : erreur opératoire, erreur provoquée par les grandeurs d'influences (température, pression etc), erreur de référence ou d'étalonnage, erreur d'hystérésis, erreur de finesse etc.
La justesse
L'erreur de justesse est l'erreur globale résultant de toutes les causes pour chacun des résultats de mesure pris isolément. C'est donc l'aptitude de l'appareil à donner des résultats qui ne sont pas entachés d'erreur.
Dans le cas de mesures multiples c'est l'écart entre le résultat moyen et la valeur vraie.
-
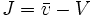
-
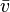
- V: Valeur vraie (ou conventionellement vraie)
Si l'on effectue une représentation en deux dimensions en considérant la valeur vraie comme l'origine on peut considérer l'erreur de justesse comme le barycentre de l'ensemble des mesures.
La fidélité
Définition : La fidélité est l'aptitude d'un appareil de mesure à donner des mesures exemptes d'erreurs accidentelles.
La fidélité définit la dispersion des résultats. Si on n'effectue qu'une seule mesure, la fidélité représente la probabilité qu'elle soit représentative du résultat moyen. Ce dernier aurait été obtenu en effectuant une infinité de mesures.
Nota : le résultat moyen étant lui-même entaché de l'erreur de justesse.
Si on effectue un ensemble de mesures d'une grandeur G, on obtient une valeur maximum (Vmax) et une valeur minimum (Vmin). Les erreurs limites de fidélité sont alors :
Exemple :
Des mesures répétées à l'aide d'un voltmètre donnent
- Umax = 100,2V
- Umin = 99,7V
-
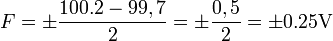
Conclusion
On peut représenter symboliquement la fidélité, la justesse et la précision de la manière suivante :