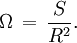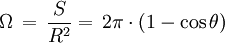Angle solide - Définition
En mathématiques, en géométrie et en physique, un angle solide est l'analogue tridimensionnel de l'angle plan ou bidimensionnel.
L'angle plan est le rapport de la longueur de l'arc sur le rayon. L'angle solide est dans l'espace le rapport de la surface d'une partie d'une sphère sur le rayon au carré. Son unité est le stéradian noté sr.
On le note souvent Ω (oméga majuscule). Il mesure la surface sur laquelle un objet se projette radialement sur une sphère de rayon unité.
Calcul
Pour calculer l'angle solide sous lequel on voit un objet à partir d'un point, on projette l'objet sur une sphère de rayon R centrée en ce point.
Si la surface que cette projection fait sur la sphère est S, l'angle solide sous lequel l'observateur voit l'objet est par définition :
La notion d'angle solide intervient en particulier dans la définition de la luminosité.
Quelques exemples
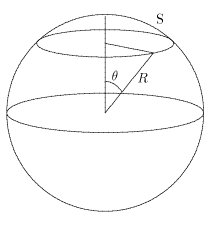
L'angle solide sous lequel on voit, du centre de la sphère, une calotte sphérique de surface S dont le diamètre apparent s'étend sur un angle de 2θ s'écrit :
Les angles θ = π/3 et θ = 2π/3 délimitent un découpage de la sphère en quatre surfaces égales de π stéradians. Ainsi, l'espace complet est vu sous un angle solide de 4π sr.
- D'un point de la surface terrestre on ne peut voir que la moitié de l'espace, c'est-à-dire une demi-sphère ou un hémisphère, soit un angle solide de 2π sr.
- Un trièdre formé par deux murs perpendiculaires et le sol décrit un angle solide de π/2 stéradians, soit un huitième de sphère.
- Entre la latitude de San Diego, en Californie, dans l'hémisphère Nord et celle de Sydney, en Australie, dans l'hémisphère Sud, il y a la moitié de la surface terrestre.
- Entre le cercle polaire et le tropique du Cancer dans l'hémisphère Nord il y a le quart de la surface terrestre, soit un angle solide de π stéradians.
- Les angles solides sous lesquels on voit une pièce d'un centime d'euro à 1,80 m de distance, la Lune et le Soleil sont très proches (≈ 6.10-5 sr).
- Un " carré de ciel " de 0,923… radians de côté se voit sous un angle solide d'un stéradian.