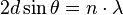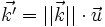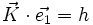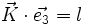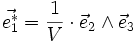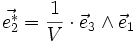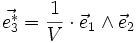Condition de diffraction pour un cristal - Définition
Lorsque l'on bombarde un cristal avec un rayonnement dont la longueur d'onde est de l'ordre de la distance inter-atomique il se produit un phénomène de diffraction. Les conditions de diffraction sont les directions dans lesquelles il y a de l'intensité.
Les rayonnements peuvent être électromagnétiques — pour cet ordre de grandeur de longueur d'onde, ce sont des rayons X — ou bien des particules ayant une énergie cinétique adaptée, de l'ordre de 100 keV pour des électrons, ou bien des dizaines de MeV pour des neutrons.
Diffraction sur un cristal
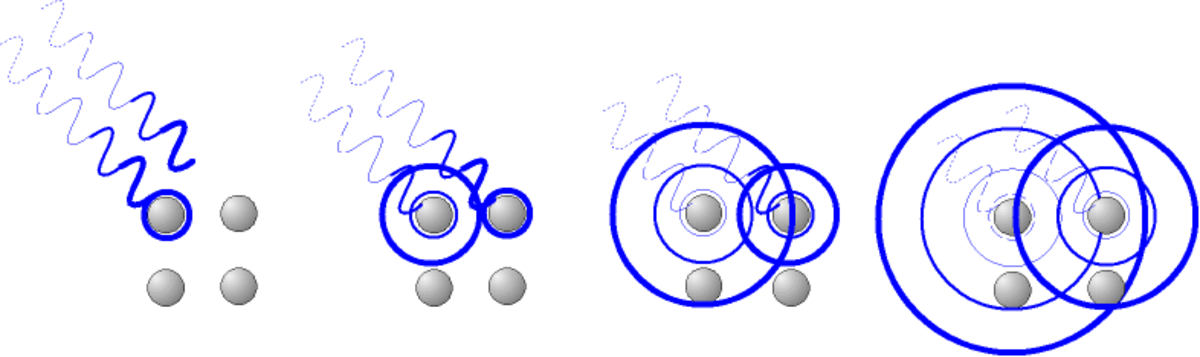
Considérons un monocristal bombardé de rayons X. Les rayons X frappent chaque atome avec une phase différente (ils parcourent un chemin optique plus ou moins long).
Les rayons X, comme toutes les ondes électromagnétiques, provoquent un déplacement du nuage électronique par rapport au noyau dans les atomes ; ces oscillations induites provoquent une réémission d'ondes électromagnétiques de même fréquence ; ce phénomène est appelé diffusion Rayleigh.
Voir aussi l'article détaillé Interaction rayonnement-matière.
Les ondes n'ont pas toutes la même phase lorsqu'elles frappent les atomes. En un point de l'espace, les ondes électromagnétiques proviennent de tous ces atomes et subissent encore un déphasage dû à la différence de chemin optique. Du fait de l'organisation régulière du cristal, dans certains endroits de l'espace, les ondes s'annulent (interférences destructives), et dans d'autres, les ondes s'additionnent et l'on a une intensité positive. Ces lieux d'intensité positive sont alignés par rapport au " point d'impact " du faisceau incident, on parle donc de " directions de diffraction ".
On peut retrouver ces directions de diffraction grâce à différentes lois équivalentes.
Loi de Bragg
La loi de Bragg est la loi régissant la diffraction des radiations sur un cristal. Elle fut découverte par W.H. et W.L. Bragg vers 1915.
Énoncé
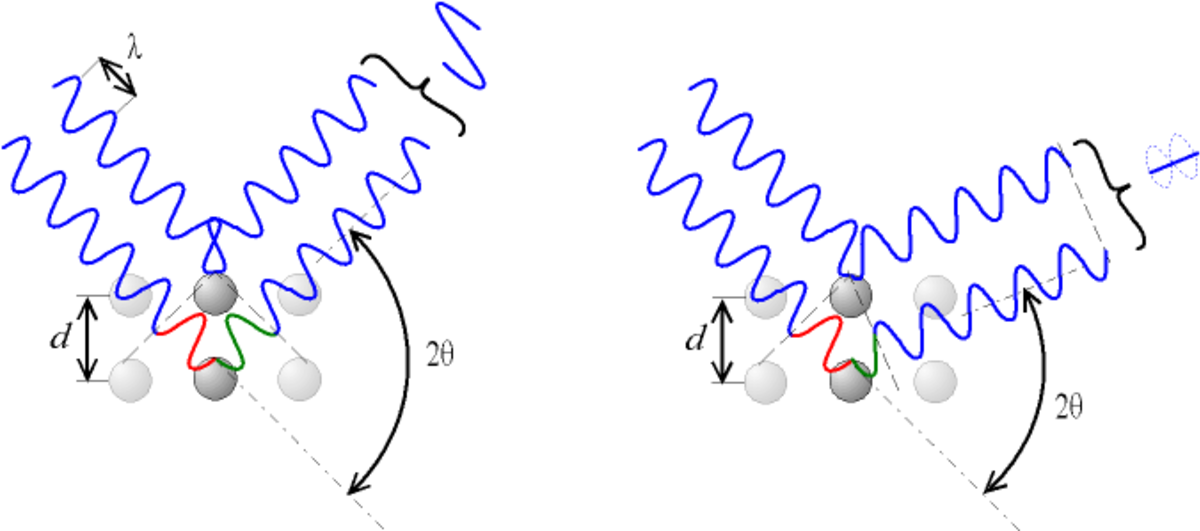
Pour cette loi, on considère des plans imaginaires contenant des atomes et perpendiculaires au vecteur de diffraction (c'est-à-dire à la bissectrice entre le faisceau incident et la direction à laquelle on s'intéresse). Mais il existe aussi d'autres lois décrivant la diffraction.
Si λ est la longueur d'onde de la radiation et d est la distance interréticulaire du plan cristallin diffractant, alors les directions 2θ de l'espace dans lesquelles on aura des pics d'intensité (le 0 pour 2θ étant la direction du faisceau incident) vérifient :
avec :
- d = distance interréticulaire, c'est-à-dire distance entre deux plans cristallographiques ;
- θ = demi-angle de déviation (moitié de l'angle entre le faisceau incident et la direction du détecteur) ;
- n = ordre de diffraction (nombre entier) ;
- λ = longueur d'onde des rayons X.
Lorsque le rayonnement n'est pas électromagnétique mais particulaire, la diffusion Rayleigh n'est pas due au déplacement du nuage atomique mais résulte du principe d'incertitude d'Heisenberg : comme la particule est bien localisée (elle interagit avec l'électron), l'incertitude sur son impulsion, donc notamment sa direction, est grande, il y a donc une diffusion isotrope. Pour bien comprendre ceci, il faut également bien comprendre la notion de dualité onde-particule.
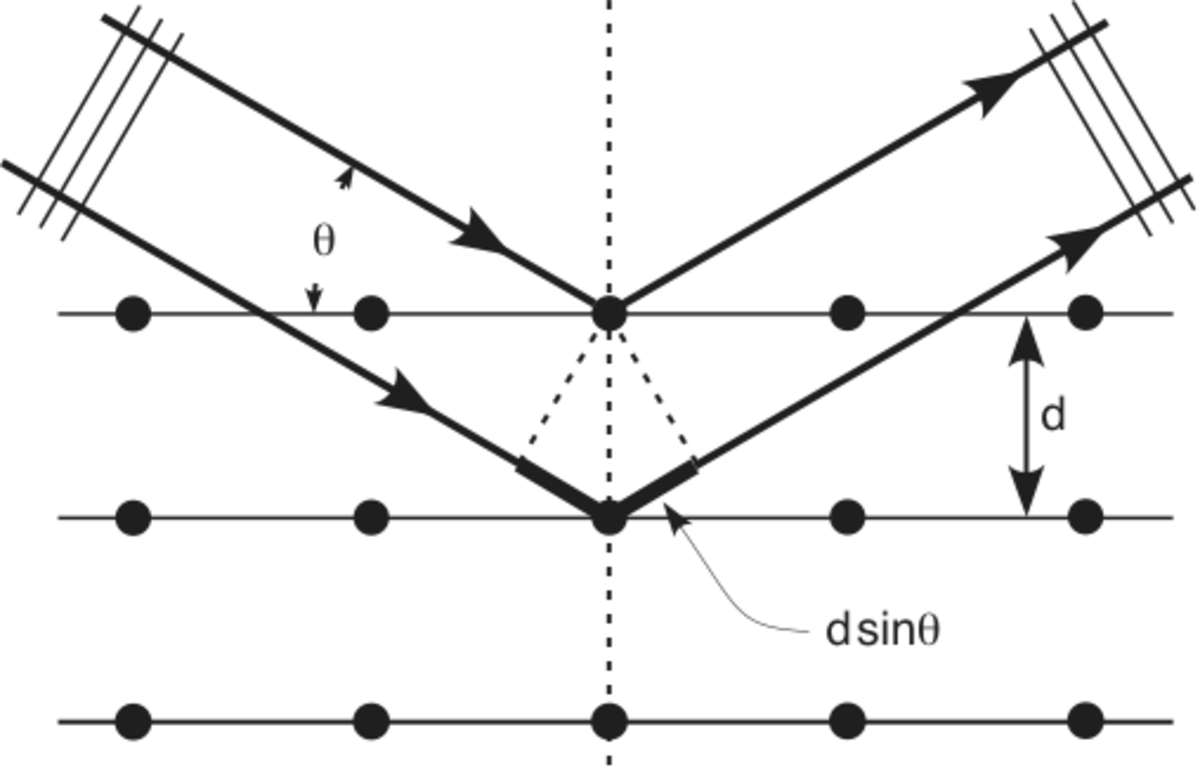
Démonstration
On peut retrouver la loi de Bragg de manière simple. Considérons deux rayons parallèles frappant deux atomes situés sur une même droite perpendiculaire à la surface. Le chemin supplémentaire parcouru par le rayon " profond " est 2d·sin(θ), puisque c'est ce trajet supplémentaire suit les côtés opposés à un angle θ de triangles rectangles d'hypoténuse d. Les interférences sont constructives si la différence de chemin introduit un déphasage multiple de 2π, c'est-à-dire si le chemin supplémentaire est un multiple de λ.
Analogie
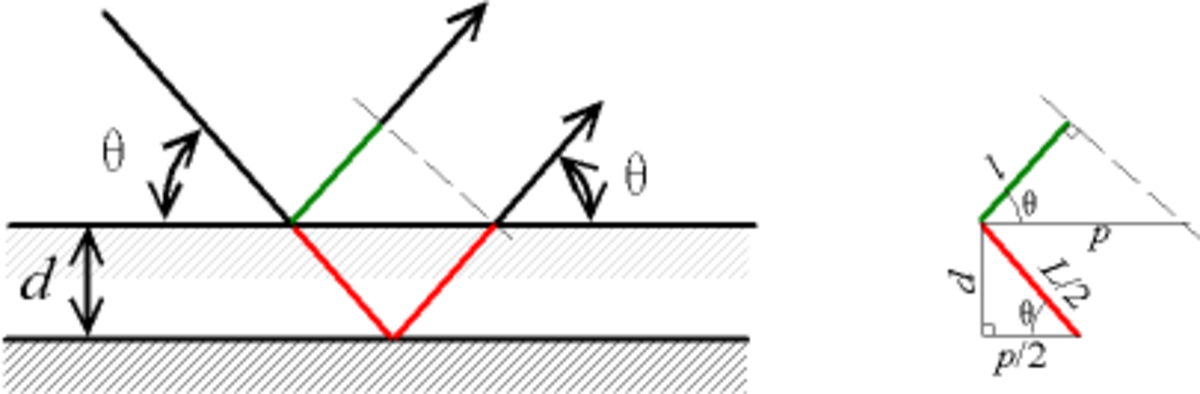
On image souvent cette loi en considérant que les plans cristallographiques sont des miroirs semi-transparents ; en effet, la formule est strictement identique aux interférences par une lame d'air que l'on obtient avec un interféromètre de Michelson. Cependant, il faut bien comprendre que les plans cristallographiques ne sont qu'une vue de l'esprit, et que dans les faits, les ondes sont diffusées individuellement par les atomes.
Condition de Laue
Le rayonnement incident a un vecteur d'onde

Si l'on s'intéresse à l'intensité diffusée dans une direction de l'espace

en effet, puisque la diffusion est élastique, la longueur d'onde reste la même, donc les vecteurs d'onde ont la même norme.
La maille élémentaire du cristal est définie par trois vecteurs
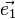
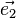
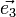
On appelle

-
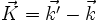
La condition de diffraction de Laue s'exprime ainsi :
- il y a diffraction dans la direction


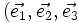
- si
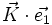
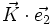
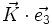
On note en général[1]
les indices (hkl) sont caractéristiques de la tâche (ou du pic) de diffraction. Ce sont aussi les indices de Miller d'un plan cristallographique, ce qui permet de retrouver le loi de Bragg.
Théorème de Bloch
On peut définir une autre base, appelée base réciproque, par[2]
Comme
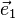
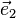
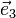
La condition de diffraction peut alors s'énoncer de la manière suivante[3] :
- il y a diffraction dans la direction


soit
-
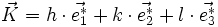
Les indices (hkl) sont les mêmes que pour la condition de Laue, et mènent donc également à la loi de Bragg.
Les points ayant des coordonnées entières dans le repère
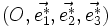
- il y a diffraction dans la direction


C'est le théorème de Bloch.
Applications
Lorsque la longueur d'onde de la radiation est de l'ordre de grandeur de la distance inter-atomique dans le cristal, les directions de diffraction sont suffisamment éloignées pour être distinguables, et suffisamment rapprochées pour figurer sur le même cliché. La loi de Bragg est utilisée entre autres pour :
- la microscopie électronique en transmission ;
- l'analyse dispersive en longueur d'onde ;
- la diffraction de rayons X
- la diffraction de neutrons
Note
- ↑ il existe deux manières de définir le vecteur d'onde ; soit sa norme est 1/λ, on a alors les formules indiquées ; soit sa norme est 2π/λ et on a alors
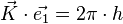
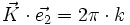
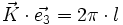
- ↑ si l'on choisit de prendre 2π/λ pour la norme du vecteur d'onde, alors
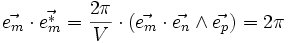
- ↑ cette condition est la même quelle que soit la définition de la norme du vecteur d'onde