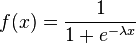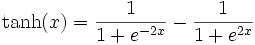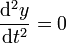Sigmoïde (mathématiques) - Définition

La fonction sigmoïde avec λ = 5.

Définition

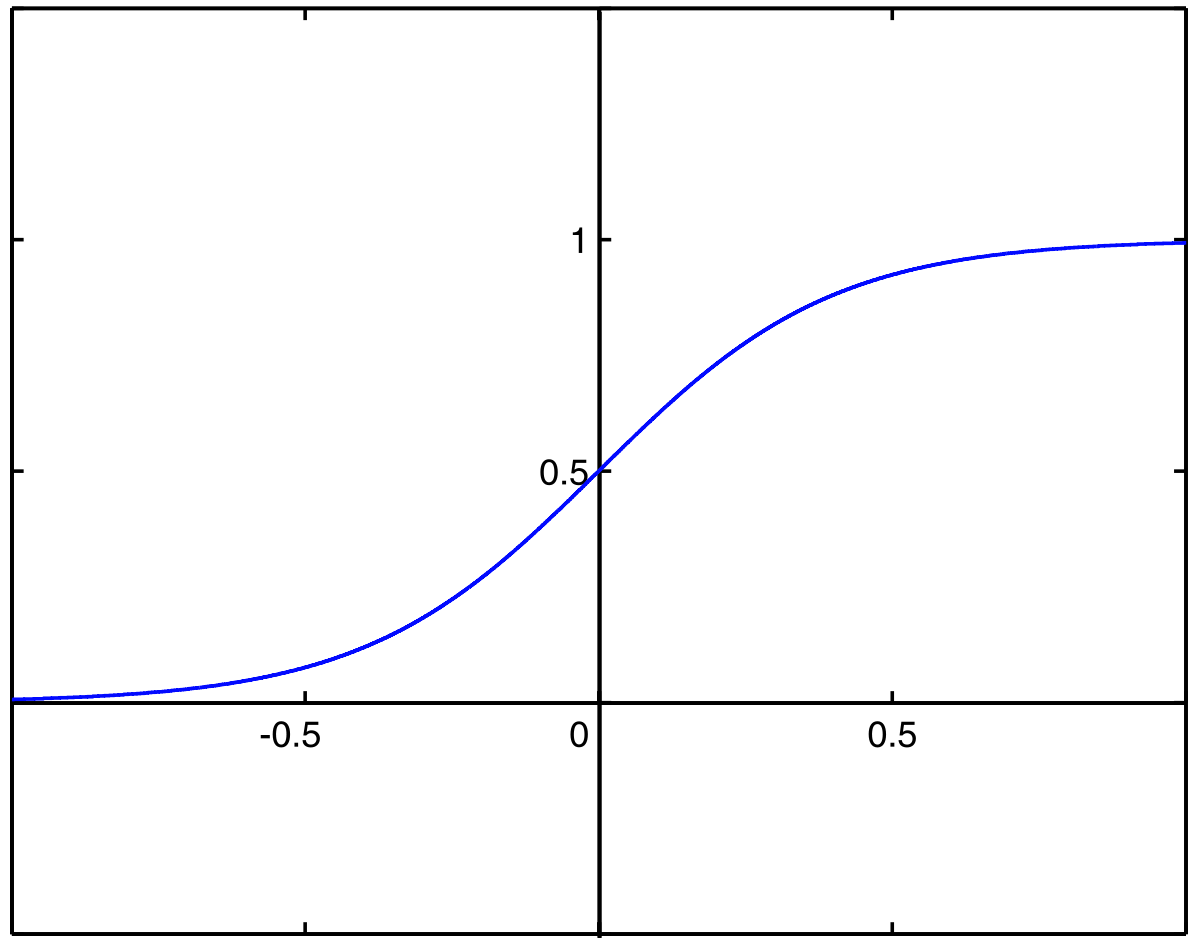
En mathématiques, la fonction sigmoïde est définie par :

Elle est symétrique par rapport au point (0; ½) : c'est son point d'inflexion, qui vérifie . Elle tend vers 0 quand x tend vers et vers 1 quand x tend vers (cf. asymptote).

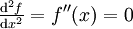
Elle est souvent utilisée dans les réseaux de neurones.

Alternative

Une alternative est la fonction tangente hyperbolique qui a la même forme mais dont les asymptotes horizontales sont en -1 et 1.

En chimie

La variation de pH d'une solution lors de réactions acido-basiques suit ce schéma. Dans ce cas, le potentiel d'acidité pKa est atteint quand :

Avec y(t) la fonction sigmoïde.

Interprétation générale concrète

Les propriétés de la fonction sigmoïde s'expliquent par celles de sa dérivée. En effet celle-ci est égale à

,

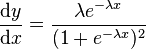
qui peut se transformer en

.

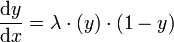
y varie de 0 à +1. Cette équation différentielle signifie que la variation de y en fonction de x (souvent le temps d'ailleurs en physique, chimie ou marketing) est proportionnelle à la fois à l'avancement de y depuis 0 et au chemin qui reste à parcourir pour arriver à 1, proportionnalité affectée d'un coefficient λ. Ceci est la forme la plus simple (simpliste peut-on dire) du modèle de contagion consumériste optimiste concernant un produit nouveau utilisé dans les études de marché : au début (temps = moins l'infini) aucun foyer ne possède de machine à laver, puis un foyer l'achète, c'est le démarrage du processus avec une proportion " epsilon " de la population. Le modèle fait les nombreuses hypothèses suivantes : le nombre de ménages est très très grand, les ménages se rencontrent aléatoirement à raison de " lambda " rencontres par jour, la géographie ne joue pas dans ces rencontres, la transformation est à sens unique (" non-équipé " vers " équipé ", jamais le contraire), le résultat d'une rencontre est le suivant : si les deux sont équipés rien ne change, si aucun n'est équipé rien ne change, si un ménage est équipé et l'autre non, alors ce dernier, convaincu par le témoignage des heureux possesseurs achète aussitôt une machine. À la fin (temps = +l'infini), tout le monde est équipé, la proportion de ménages équipés est 100%=1. Ce modèle est aussi celui de la contagion dans la bande dessinée les Schtroumpfs noirs, ainsi que dans le film La Nuit des morts-vivants (quand un vivant est mordu par un mort-vivant, il meurt puis se relève en mort-vivant, mais un mort-vivant ne redevient pas vivant-simple sous une quelconque action). C'est le modèle basique de la contagion en épidémiologie. Le calibrage de la courbe se fait par l'intermédiaire de la variable λ qui est égale à 4 fois la pente de la courbe au point d'inflexion. La dérivée seconde possède aussi quelques propriétés : elle peut se transformer en

.

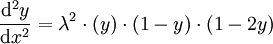
ce qui vérifie bien qu'un point d'inflexion est le point-milieu y=½. Les autres points d'inflexion sont rencontrés aux extrémités de la courbe (y=0 et y=1), il s'agit plutôt de points asymptotiques de rayon infini.