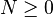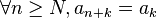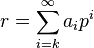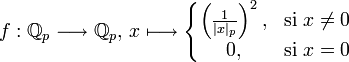Nombre p-adique - Définition
En mathématiques, un nombre p-adique est un élément du corps
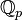
Les corps
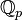

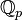

La principale motivation ayant donné naissance aux corps des nombres p-adiques était de pouvoir utiliser les techniques des séries entières dans la théorie des nombres, mais leur utilité dépasse maintenant largement ce cadre. De plus, il est possible de munir un corps
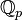
Construction
Approche analytique
Les nombres réels sont définis comme des classes d'équivalence des suites de Cauchy des nombres rationnels. Cependant, cette définition repose sur la métrique choisie et, en en choisissant une autre, d'autres nombres que les nombres réels peuvent être construits. La métrique utilisée pour les nombres réels est appelée métrique euclidienne.
Pour un nombre premier donné p, on définit la norme p-adique sur

- on rappelle que la valuation p-adique d'un entier a non nul est l'exposant de p dans la décomposition de a en produit de facteurs premiers.
- on peut alors construire une valuation pour tout nombre rationnel non nul en posant :
-
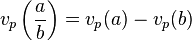
-
- On prouve aisément que cette définition est indépendante du représentant du rationnel choisi.
- la norme p-adique | r | p d'un rationnel r non nul vaut
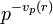
- si r est nul, on pose | r | p = 0. Ce prolongement est compatible avec l'idée que 0 est divisible par pk pour toute valeur de k, donc que la valuation de 0 serait infinie.
En quelque sorte, plus r est divisible par p, plus sa norme p-adique est petite (c'est un cas particulier de valuation discrète un outil algébrique !).
Par exemple, pour
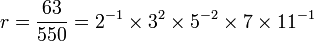
-
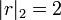
-
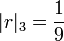
-
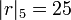
-
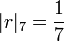
-
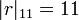
-
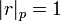
On démontre que cette application a toutes les propriétés d'une norme. On peut montrer que toute norme (non-triviale) sur


- dp(x,y) = | x − y | p
Le corps
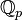


Cette construction permet de comprendre pourquoi
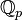

Approche algébrique
Dans cette approche algébrique, on commence par définir l'anneau des entiers p-adiques, puis par construction le corps des fractions de cet anneau pour obtenir le corps des nombres p-adiques.
On définit l'anneau des entiers p-adiques
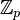
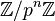
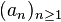
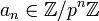
Par exemple, 35 en tant que nombre 2-adique serait la suite
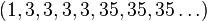
L'addition et la multiplication de telles suites sont bien définies, puisqu'elles commutent avec l'opérateur modulo (voir arithmétique modulaire). De plus, toute suite (an) dont le premier élément n'est pas nul a un inverse.
L'anneau des entiers p-adiques ne possédant pas de diviseurs de zéro, il est possible de considérer son corps des fractions pour obtenir le corps
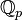
Décomposition canonique de Hensel
Soit p un nombre premier. Tout élément non nul r de
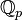

où
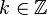
Cette série est convergente suivant la métrique p-adique.
On note
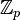
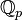
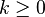
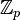
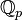
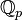
Par exemple, avec p = 2 :
-
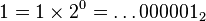
-
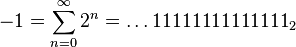
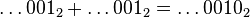
-
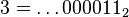
-
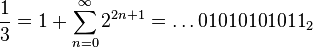
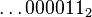
-
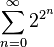
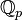
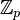
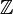
Un autre exemple, avec p = 7 :
2 n'a pas de racine carrée dans

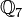
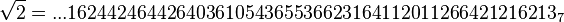
Propriétés
Dénombrabilité
L'ensemble des entiers p-adiques n'est pas dénombrable.
Les nombres p-adiques contiennent les nombres rationnels et forment un corps de caractéristique nulle. Il n'est pas possible d'en faire un corps ordonné.
Topologie
La topologie sur l'ensemble des entiers p-adiques est celle de l'ensemble de Cantor; la topologie sur l'ensemble des nombres p-adiques est celle de l'ensemble de Cantor privé d'un point (qui serait naturellement appelé infini). En particulier, l'espace des entiers p-adiques est compact, tandis que l'espace des nombres p-adiques ne l'est que localement. En tant qu'espaces métriques, les entiers et les nombres p-adiques sont complets.
Les nombres réels n'ont qu'une seule extension algébrique propre, les nombres complexes. En d'autres termes, cette extension quadratique est algébriquement close. La clôture algébrique des nombres p-adiques est infinie. Les corps
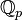
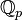
Le corps Ωp, aussi noté
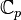

Les nombres p-adiques contiennent le ne corps cyclotomique si et seulement si n divise p − 1. Par exemple, les 1er, 2e, 3e, 4e, 6e et 12e corps cyclotomiques sont des sous-corps de
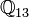
Le nombre e n'est élément d'aucun des corps p-adiques. Cependant, ep est un nombre p-adique, sauf si p = 2. e est un élément de la clôture algébrique de tous les corps p-adiques.
Sur les nombres réels, les seules fonctions dont les dérivées sont nulles sont les fonctions constantes. Ceci n'est pas vrai sur les nombres p-adiques. Par exemple, la fonction
possède une dérivée nulle en tous points, mais n'est même pas constante localement en 0.
Si on se donne les éléments
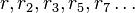
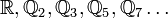


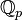
Rationalité
Un nombre positif γ0 est rationnel si, et seulement si, son développement p-adique est périodique à partir d'un certain rang, c'est-à-dire, s'il existe 2 entiers