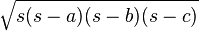Aire de surfaces usuelles - Définition

La notion d'aire d'une surface se définit en géométrie euclidienne en dimension 2 ou 3 et est supposée connue du lecteur. L'aire des surfaces usuelles s'exprime à l'aide de formules simples. On peut estimer l'aire d'une surface aux contours compliqués en sommant des aires de surfaces plus simples. Ce point de vue débouche sur le calcul des intégrales. Le théorème de Guldin permet de calculer aisément l'aire de surfaces de révolution.

Aire de surfaces planes

Nom de la surface	Description	Paramètres	Aire	Nom de la formule
Carré	Quadrilatère aux angles et côtés égaux	Longueur a d'un des côtés	a2
Rectangle	Quadrilatère aux angles droits	Longueurs a at b des côtés	a.b
Triangle	Donnée de trois points A B C non colinéaires du plan	Hauteur h en B et longueur b du segment opposé [AC]	(b × h) / 2
		Longueurs a b et c des côtés et demi-périmètre s		Formule de Héron
Trapèze	Quadrilatère possédant deux côtés opposés parallèles, ses bases	Longueur a et b des bases et distance h entre elles	((a + b)*h)/2
Losange	Quadrilatère dont les côtés opposés sont parallèles et égaux	Longueurs a et b de ses diagonales	(a × b) / 2
Parallélogramme	Quadrilatère dont les côtés opposés sont parallèles	Longueurs a et b des côtés adjacents et mesure θ de l'angle qu'ils forment	a × b × sin(θ)
		Longueur b d'un côté du parallélogramme et longueur h de la hauteur associée	b × h
Disque	Ensemble des points à une distance du centre inférieure ou égale au rayon	Rayon r	π × r²
Ellipse	Ensemble des points tels que la somme de leurs distances à deux points fixes, dits foyers, est constante	Longueurs a et b des demi-axes	π × a × b

Aire en dimension 3