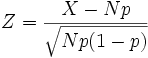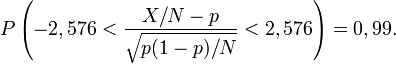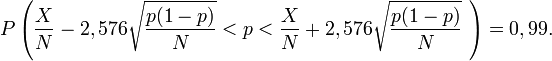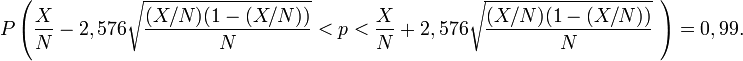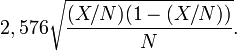Marge d'erreur - Définition
En statistiques, la marge d'erreur est une estimation de l'étendue que les résultats d'un sondage peuvent avoir si l'on recommence l'enquête. Plus la marge d'erreur est importante, moins on peut avoir confiance que les résultats du sondage sont proches des vrais résultats, et ainsi, de la réalité.
La marge d'erreur peut être calculée directement à partir de la taille de l'échantillon (par exemple, le nombre de personnes sondées) et est habituellement reportée par l'un des trois différents niveaux de l'intervalle de confiance. Le niveau de 99% est le plus prudent, le niveau de 95% est le plus répandu, et le niveau de 90% est rarement utilisé. Pour un niveau de confiance de 99%, on est sûr à 99% que la vraie valeur se trouve dans la marge d'erreur de la valeur issue du sondage.
Il est à noter que la marge d'erreur prend uniquement en compte l'erreur de l'échantillon. Elle ne prend pas en compte les autres sources potentielles d'erreurs, notamment, le biais dans les questions ou dans l'exclusion d'un groupe n'étant pas questionné, le fait que certaines personnes ne veulent pas répondre, le fait que certaines personnes mentent, les erreurs de calculs.
Calculs
La marge d'erreur est une simple reformulation de la taille de l'échantillon, N. Les numérateurs des équations suivantes sont arrondies à la deuxième décimale.
- Marge d'erreur à 99%
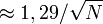
- Marge d'erreur à 95%
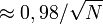
- Marge d'erreur à 90%
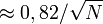
La marge d'erreur n'est pas complétement définie si l'intervalle de confiance n'est pas rapportée. Si un article à propos d'un sondage ne donne pas l'intervalle de confiance, la marge d'erreur peut être approximée pour le degré de confiance désiré à l'aide de la taille de l'échantillon. De plus, si la marge d'erreur à 95% est donnée, il est possible de calculer la marge d'erreur à 99% en l'augmentant d'environ 30%.
Compréhension
Exemple
Pour illustrer les concepts expliqués au cours de l'article, nous utiliserons l'exemple de la campagne présidentielle des États-Unis de 2004. Selon un sondage paru dans Newsweek, 47% des électeurs voteraient pour John Kerry si l'élection avait lieu aujourd'hui. 45% voteraient pour George W. Bush et 2% pour Ralph Nader. La taille de l'échantillon est de 1 013 personnes interrogées, et la marge d'erreur est de ±4%. Dans le reste de l'article, nous utiliserons l'intervalle de confiance de 99%.
Concept de base
Un sondage nécessite de prendre un échantillon de la population. Dans le cas du sondage de Newsweek, la population prise en compte sont les personnes qui voteront. Étant donné l'impossibilité d'interroger tous les électeurs, les instituts de sondage construisent des échantillons qui sont normalement représentatif de la population. Il est possible qu'ils interrogent 1 013 personnes qui vont voter pour Bush alors que dans la réalité les électeurs sont partagés, mais c'est très peu probable si l'échantillon est suffisamment représentatif de la population.
Termes statistiques et calculs
La marge d'erreur est juste un intervalle de confiance de 99%, qui revient donc à une simple transformation de l'écart-type du résultat. Cette section discute brièvement l'écart-type d'un résultat, l'intervalle de confiance et lie ces deux concepts à la marge d'erreur.
L'écart-type peut être estimée simplement étant donné une proportion ou un pourcentage, p, et le nombre de personnes enquêtées, N. Dans le cas du sondage commandé par Newsweek, le pourcentage de vote pour Kerry, p=0,47 et N=1 013. Selon des théories statistiques présentées ci-dessous,
- Écart-type =
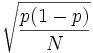
Plus ou moins 1 écart-type est un intervalle de confiance de 68%, plus ou moins 2 écart-type est approximativement un intervalle de confiance de 95%, et un intervalle de confiance de 99% est un écart-type de 2,58 de chaque de côté de la valeur estimée. adel
- Marge d'erreur (99%) = 2,58 ×
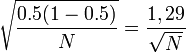
Comparaison des pourcentages
Tables
La marge d'erreur est fréquemment utilisée d'une mauvaise façon pour déterminer si un pourcentage est supérieur à un autre. La statistiques qui doit être utilisé dans ce cas est simplement la probabilité qu'un pourcentage soit supérieur à un autre. Le tableau ci-dessous présente les " probability of leading " de deux candidats, en l'absence d'autres candidats, et en prenant un niveau de 95 % de confiance:
| Différence de pourcentages : | 0% | 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1% marge d'erreur | 50.0 | 83.6 | 97.5 | 99.8 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 2% marge d'erreur | 50.0 | 68.8 | 83.7 | 92.9 | 97.5 | 99.3 | 99.8 | 100 | 100 | 100 | 100 |
| 3% marge d'erreur | 50.0 | 62.8 | 74.3 | 83.7 | 90.5 | 94.9 | 97.5 | 98.9 | 99.6 | 99.8 | 99.9 |
| 4% marge d'erreur | 50.0 | 59.7 | 68.8 | 76.9 | 83.7 | 89.0 | 93.0 | 95.7 | 97.5 | 98.7 | 99.3 |
| 5% marge d'erreur | 50.0 | 57.8 | 65.2 | 72.2 | 78.4 | 83.7 | 88.1 | 91.5 | 94.2 | 96.2 | 97.6 |
| 6% marge d'erreur | 50.0 | 56.5 | 62.8 | 68.8 | 74.3 | 79.3 | 83.7 | 87.4 | 90.5 | 93.0 | 95.0 |
| 7% marge d'erreur | 50.0 | 55.6 | 61.0 | 66.3 | 71.2 | 75.8 | 80.0 | 83.7 | 86.9 | 89.7 | 92.0 |
| 8% marge d'erreur | 50.0 | 54.9 | 59.7 | 64.3 | 68.8 | 73.0 | 76.9 | 80.5 | 83.7 | 86.6 | 89.1 |
| 9% marge d'erreur | 50.0 | 54.3 | 58.6 | 62.8 | 66.9 | 70.7 | 74.4 | 77.8 | 80.9 | 83.7 | 86.3 |
| 10% marge d'erreur | 50.0 | 53.9 | 57.8 | 61.6 | 65.3 | 68.8 | 72.2 | 75.4 | 78.4 | 81.2 | 83.8 |
Par exemple, la probabilité que John Kerry gagne face à Georges Bush selon les données du sondage de Newsweek (une différence de 2% et une marge d'erreur de 4%) est d'environ 68,8%, à condition qu'ils aient utilisé un niveau de 95% de confiance. Voici la même table pour un niveau de 99% de confiance:
| Différence de pourcentages : | 0% | 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1% marge d'erreur | 50.0 | 90.1 | 99.5 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 2% marge d'erreur | 50.0 | 74.1 | 90.2 | 97.4 | 99.5 | 99.9 | 100 | 100 | 100 | 100 | 100 |
| 3% marge d'erreur | 50.0 | 66.6 | 80.5 | 90.2 | 95.7 | 98.4 | 99.5 | 99.9 | 100 | 100 | 100 |
| 4% marge d'erreur | 50.0 | 62.6 | 74.1 | 83.3 | 90.2 | 94.7 | 97.4 | 98.8 | 99.5 | 99.8 | 99.9 |
| 5% marge d'erreur | 50.0 | 60.2 | 69.7 | 78.1 | 84.9 | 90.2 | 94.0 | 96.5 | 98.1 | 99.0 | 99.5 |
| 6% marge d'erreur | 50.0 | 58.5 | 66.6 | 74.1 | 80.5 | 85.9 | 90.2 | 93.4 | 95.8 | 97.4 | 98.5 |
| 7% marge d'erreur | 50.0 | 57.3 | 64.4 | 71.0 | 77.0 | 82.2 | 86.6 | 90.2 | 93.0 | 95.2 | 96.8 |
| 8% marge d'erreur | 50.0 | 56.4 | 62.6 | 68.6 | 74.1 | 79.0 | 83.4 | 87.1 | 90.2 | 92.7 | 94.7 |
| 9% marge d'erreur | 50.0 | 55.7 | 61.3 | 66.6 | 71.7 | 76.3 | 80.6 | 84.3 | 87.5 | 90.2 | 92.5 |
| 10% marge d'erreur | 50.0 | 55.1 | 60.2 | 65.1 | 69.7 | 74.1 | 78.1 | 81.7 | 85.0 | 87.8 | 90.3 |
Si le sondage réalisé pour Newsweek utilise un niveau de 99% de confiance, alors la probabilité que Kerry gagne face à Bush serait de 74,1%. Dès lors, il semble évident que le niveau de confiance a un impact significatif sur la probabilité de gagner.
Calculs avancés
Soit N le nombre de votants dans l'échantillon. Supposons qu'ils ont été tirés de façon aléatoire et indépendante de la population totale. L'hypothèse est peut être trop forte, mais si la constitution de l'échantillon est faite avec soin la réalité peut au moins s'approcher de cette situation. Soit p la proportion de votants de la population totale qui voteront " oui ". Alors le nombre X de votants de l'échantillon qui voteront " oui " est une variable aléatoire distribuée selon une loi binomiale de paramètres N et p. Si N est suffisamment grand, alors X suit la loi normale de moyenne Np et de variance Np(1 − p). Donc
suit la loi normale centrée réduite (celle qui a pour paramètres 0 et 1).
La table de la loi normale révèle que P(−2,576 < Z < 2,576) = 0,99, ou, en d'autres termes, qu'il y a 99 chances sur cent pour que cet événement se réalise. Ainsi,
Cela équivaut à
En remplaçant p dans le premier et le troisième membre de cette inégalité par la valeur estimée X/N débouche rarement sur des erreurs importantes si N est assez grand. Cette opération se traduit par:
Le premier et le troisième membre de l'inégalité dépendent de la valeur observable X/N et de la valeur inobservable p, et sont les valeurs extrêmes de l'intervalle de confiance. Autrement dit, la marge d'erreur est