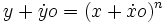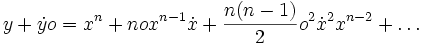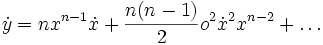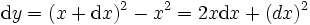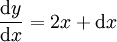Histoire du calcul infinitésimal - Définition
L'histoire du calcul infinitésimal est liée à deux mathématiciens : Isaac Newton et Gottfried Wilhelm von Leibniz.
Contexte
Au XVIIe siècle, deux problèmes passionnent les mathématiciens : celui de la tangente et celui des quadratures. Le premier consiste à retrouver, à partir d’une courbe quelconque, les différentes tangentes à la courbe. Le deuxième réside dans le calcul de l'aire engendrée par une courbe. Nombreux sont ceux qui s’intéressent à ces problèmes et en donnent diverses solutions : Descartes, Wallis, et d’autres. Cependant, deux scientifiques, Isaac Newton et Leibniz, vont chacun de leur côté faire des recherches et mettre au jour une solution générale et simple à ces problèmes. Ce faisant, ils introduiront dans le monde des mathématiques un nouveau concept qui est aujourd’hui la base de l’analyse : le calcul infinitésimal.
Isaac Newton
Grand mathématicien et physicien anglais du XVIIe siècle, Newton est considéré comme l’un des fondateurs du calcul infinitésimal. S’inspirant de Descartes et Wallis dont il avait lu les écrits, il se pose en effet le problème des tangentes qu’il relie rapidement à celui de la quadrature. Cependant, il écrit assez peu sur ce sujet (seulement trois écrits) et sera publié très tard par peur des critiques. Dès 1669, Newton, s’inspirant de Wallis et Barrow, relie le problème de la quadrature à celui des tangentes : la dérivée est la procédure inverse de l'intégration. Il s’intéresse aux variations infinitésimales des quantités mathématiques et l’aire engendrée par ces mouvements. Sa méthode la plus célèbre reste celle des fluxions. Très influencé par son travail de physicien, il considère les quantités mathématiques comme engendrées " par une augmentation continuelle " et les compare à l’espace engendré par les " corps en mouvement ". Dans le même esprit, il introduit le temps en tant que variable universelle et définit les fluxions et les fluentes. Les fluentes (x, y, z, …) sont des quantités " augmentées graduellement et indéfiniment ", et les fluxions (
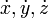
Voici par exemple la solution qu’il donne pour y = xn :
- Soit o, un intervalle de temps infiniment petit.
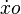
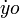
-
- En remplaçant x et y par
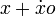
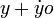
-
- Puis en développant par la formule du binôme qu’il a démontrée :
-
- Ensuite, il retranche
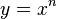
-
- Enfin, il néglige tous les termes contenant o, et obtient :
-
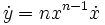
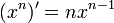
-
L’intuition est bien là, mais Newton manque de conviction. Il voudrait se débarrasser des quantités infinitésimales qu’il n’arrive pas à baser sur des principes rigoureux. Dans sa méthode " des premières et dernières raisons ", il se contentera des rapports entre fluxions, ce qui lui permettra d’éviter de " négliger " des termes, laissant o " s’évanouir " dans le rapport. Il se rapproche alors de notre notion actuelle de limite, comparant cela à l’idée de " vitesse instantanée " d’un corps. Non pas celle qu’il a avant d’arriver, ni celle qu’il a après, mais celle qu’il a au moment où il arrive. Dans Principia, il exprime ainsi sa pensée : " Les rapports ultimes dans lesquels les quantités disparaissent ne sont pas réellement des rapport de quantités ultimes, mais les limites vers lesquels les rapport de quantités, décroissant sans limite, s’en approchent toujours : et vers lesquels ils peuvent s’en approcher aussi près que l’on veut. " Il est incroyable de voir à quel point cette conception se rapproche de la définition même de la limite utilisée aujourd’hui : f(x) tend vers a si étant donné ε donné positif quelconque, il existe α tel que : |x-a|<α => |f(x)-f(a)|<ε. Cependant, Newton ne généralise pas cette définition et sa notion de limite reste réservée aux rapports de fluxions, à ce qui se rapproche de notre calcul de dérivées. Et même ainsi, il se trouve dans l’incapacité de fonder son calcul différentiel sur des bases rigoureuses. La notion de valeur infinitésimale est encore trop nouvelle et se trouve vivement critiquée, n’étant pour certains qu’un " fantôme de quantités disparues ".
Gottfried Wilhelm von Leibniz
Alors que Newton hésitait à publier ses découvertes, un autre mathématicien : Wilheilm Leibniz s’intéressait à ce même problème et fit des découvertes semblables. Son approche est cependant très différente. En effet, Leibniz est au départ un philosophe et ne découvre les mathématiques qu’en 1672 lorsqu’il rencontre Christian Huygens lors d’un voyage à Paris. Il s’inspire alors des œuvres de Descartes, Pascal, Wallis et d’autres. Très vite, il fait le lien entre le problème des tangentes et celui de la quadrature en remarquant que le problème de la tangente dépend du rapport des " différences " des ordonnées et des abscisses et celui de la quadrature, de la " somme " des ordonnées. Lors de son travail sur les combinatoires, il observe en effet ceci :
- 1, 4, 9, 16 étant la suite des carrés
- 1, 3, 5, 7 la suite des différences des carrés :
- 1+3+5+7=16
Son travail en philosophie le pousse à considérer les différences infiniment petites et il tire bientôt la conclusion : ∫dy = y , ∫ étant une somme de valeurs infiniment petites et dy une différence infinitésimale.
En effet, Leibniz émet à la même époque l’hypothèse philosophique de l’existence de composants infiniment petits de l’univers. Tout ce que nous percevons n’étant que la somme de ces éléments. Le rapport avec ces recherches mathématiques est direct. Il explique parfois aussi ces éléments infinitésimaux en faisant une analogie avec la géométrie : le dx est au x, ce que le point est à la droite. Ce qui le pousse dans l’hypothèse de l’impossibilité de comparer des valeurs différentielles à de " vraies " valeurs. Tout comme Newton, il privilégiera les comparaisons entre rapport. La notation claire et pratique qu’il met en place (celle que nous utilisons aujourd’hui) permet des calculs rapides et simples. S’intéressant au rapport dy/dx, il l’identifie au coefficient directeur de la tangente, se justifiant par l’étude du triangle formé par une portion infiniment petite de la tangente et deux portions infiniment petites des parallèles à l’axe des abscisses et à celui des ordonnées. Ainsi, il exprime par exemple le coefficient directeur de la tangente à la courbe représentative de y=x² :
Et enfin, en négligeant dx :
-
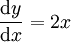
Il résout aussi les problèmes d(x + y), d(x.y), d(x/y), d(x?) dans l’optique de créer une véritable algèbre des infiniment petits. Mais il subit de nombreuses critiques, semblables à celle que l’on fit à Newton : Pour quelle raison néglige-t-on les infinitésimaux dans le résultat final ? Et si ils sont égaux à 0, comment peut-on faire leur rapport ? Lui-même a du mal à baser sa théorie sur des concepts solides et a tendance à considérer les valeurs infinitésimales comme des outils, au même titre que les nombres imaginaires, qui " n’existeraient " pas vraiment. Mais même ainsi, ses détracteurs restent nombreux.
Au XIXe siècle
Ce n’est qu’au XIXe siècle que le concept de limite sera véritablement explicité. Et c’est seulement ainsi que le calcul différentiel pourra vraiment se développer. Car, en effet, ce ne sont pas sur des rapports que travaillent Newton et Leibniz, mais bien sur des limites de rapport, et c’est ce concept qui est la base de tout le reste. C’est à cette époque que le nombre réel comme nous le connaissons est véritablement introduit chez les mathématiciens. Autant chez Newton que chez Leibniz, c’est cette conception qui manque et qui les empêche de fonder la limite sur des bases rigoureuses. Le nombre comme ils le conçoivent est encore très inspiré de la vision d’Euclide. Et sans la caractérisation de la densité et du caractère intrinsèquement infini des réels, le concept de limite ne peut voir le jour.
C’est ce qui fait que leurs détracteurs, au nombre desquels George Berkeley, seront très nombreux. On accusera aussi Leibniz d’avoir copié l’œuvre de Newton. S’ensuivront de nombreuses disputes et des attaques personnelles entre les deux hommes. Nous pouvons cependant constater que leurs approches sont très différentes et c’est cette différence qui apporte toute sa richesse et toute son inventivité à ce nouveau concept. C’est aussi ces deux visions des choses, dans leurs points communs et dans leurs dissemblances, qui peuvent nous permettre, encore aujourd’hui, de mieux comprendre ce concept de valeur infinitésimale. En effet, c’est son rapport avec la physique, la philosophie ou la géométrie, qu’eux même ont dû faire pour le conceptualiser, qui nous donne la possibilité de le saisir dans son ensemble.
Malgré les critiques, les méthodes simples et claires mises au point par Newton et Leibniz, en particulier le nouveau formalisme introduit par Leibniz, permettent de résoudre les problèmes des tangentes et de la quadrature, qui préoccupaient beaucoup les mathématiciens de l’époque. Et c’est pourquoi elles se sont petit à petit fait accepter jusqu’à leur fondation sur des bases solides au XIXe siècle. Nous devons encore beaucoup, nous-même, à ces concepts, et nous utilisons encore d’ailleurs le formalisme de Leibniz de façon courante et même celui de Newton en physique. Et c’est pourquoi, encore aujourd’hui, Newton et Leibniz, au-delà de leurs querelles, sont considérés comme les fondateurs du calcul infinitésimal.