Suite (mathématiques élémentaires) - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
Intuitivement une suite réelle est une règle qui associe à chaque entier naturel n un certain nombre réel ; on dit alors que ce nombre réel est indexé par l’entier. En fait une suite est un moyen d’indexer des nombres réels par des entiers naturels, et ce de manière ordonnée.
Une suite réelle est une application de l’ensemble des entiers naturels



Soit u :
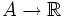
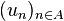
Lorsque A=


- ( u0, u1, …, un, …)
Les derniers trois petits points consécutifs signifient qu’il y a une infinité de termes après.
Si A={1,2,…, n} alors nous obtenons la suite finie, de n termes :
- ( u1, u2, …, un)
Remarquons que la notation (un) correspond à une application alors que la notation un désigne un nombre réel.
Dans la pratique, les suites sont souvent indexées sur

Donnons quelques exemples de suites :
-

-
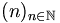
-
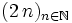
-
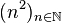
-
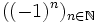
Les suites les plus étudiées en mathématiques élémentaires sont les suites arithmétiques, les suites géométriques et les suite arithmético-géométriques
Variations d’une suite
Soit
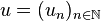
Croissance
La suite u est dite croissante si pour tout entier naturel n,
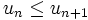
On a donc,
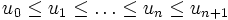
Décroissance
La suite u est dite décroissante si pour tout entier naturel n,
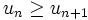
On a donc,
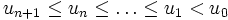
Monotonie
La suite u est monotone si elle est croissante ou décroissante. De même, la suite u est strictement monotone si elle est strictement croissante ou strictement décroissante.
Suite stationnaire
Une suite u est dite stationnaire s’il existe un rang n0 à partir duquel tous les termes de la suite sont égaux, c'est-à-dire un entier naturel n0 tel que pour tout entier naturel n supérieur à n0,
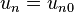
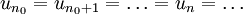
Exemples
- Si pour tout entier naturel n, un= 2n+1
-
- La suite u est croissante.
- Si pour tout entier naturel n non nul,
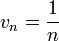
- La suite v est décroissante.
- u et v sont donc monotones (et même strictement).
- En revanche, la suite w définie par : pour tout entier naturel n, wn = ( − 1)n + 1
- n'est pas monotone en effet w0 = − 1, w1 = 1, w2 = − 1.
- Elle n'est ni croissante, ni décroissante.
- Étudier les variations d’une suite c’est déterminer si elle est croissante ou décroissante.
Donnons quelques règles pratiques permettant d’étudier les variations d’une suite
-
- on étudie pour tout entier naturel n, le signe de
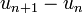
- lorsque tous les termes de la suite sont strictement positifs et qu’ils sont sous forme d’un produit, on peut étudier pour tout entier naturel n, le rapport
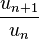
- si le terme général un et de la forme f(n) où f est une fonction définie sur
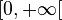
- on étudie pour tout entier naturel n, le signe de
Majorant minorant
- Suite majorée
Une suite u est dite majorée s'il existe un réel M tel que pour tout entier naturel n,
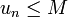
- Suite minorée
Une suite u est dite minorée s'il existe un réel m tel que pour tout entier naturel n,
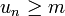
- Suite bornée
Une suite u est dite bornée si elle est à la fois majorée et minorée. Dans ce cas, il existe des réels M et m tels que pour tout entier naturel n,
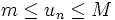
Caractère borné
u est bornée si et seulement s'il existe un réel K tel que pour tout entier naturel n,
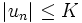
Conséquence :
Pour démontrer qu’une suite u est bornée, il suffit de monter que la suite (|un|) est majorée.
Exemples
- La suite u définie par : pour tout entier naturel n,
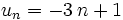
- La suite v définie par : pour tout entier naturel n, vn = (n − 7)2 est minorée par 0 mais n’est pas majorée.
- La suite w définie par : pour tout entier naturel non nul n,
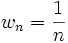
Propriétés
- Une suite croissante u est minorée par son premier terme u0.
- Une suite décroissante u est majorée par son premier terme u0.
- Lorsque le terme général un d’une suite s’écrit sous la forme d’une somme de n termes, nous pouvons minorer la somme par n fois le plus petit terme de la somme et majorer par n fois le plus grand. Mais cela ne permet pas toujours d’obtenir un minorant ou un majorant de la suite.
Erreurs fréquentes
Questions
- La suite x définie par : pour tout entier naturel n,
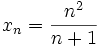
- La suite y définie par : pour tout entier naturel n,
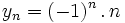
- La suite z définie par : pour tout entier naturel n non nul,
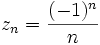
Réponses
- En effectuant le calcul suivant, on montre que tout terme de rang n est nécessairement plus petit que n:
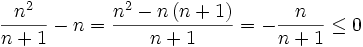
- Il suffit de voir ce que sont les premiers termes pour comprendre le fonctionnement de cette suite :
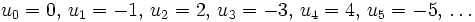
- Ici, les termes de rang (d'indice) pair sont égaux à leur inverse, et les termes de rang impair sont égaux à l'opposé de leur inverse. Cette suite est bornée et " atteint ses bornes ", c’est-à-dire que le plus petit des majorants et le plus grand des minorants (les bornes en analyse) sont des termes de la suite, ce qui n'était pas le cas avec la suite des inverses, quant à sa borne inférieure). z1 = − 1 et
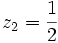
Limite, convergence, divergence
Voir l'article Limite (mathématiques élémentaires).

















































