Couple (mathématiques) - Définition

En mathématiques, un couple de deux objets est la donnée de ces deux objets dans un ordre déterminé. Le couple des deux objets a et b est noté (a,b). Si a et b sont distincts le couple (a,b) est distinct du couple (b,a). En cela la notion de couple se distingue de la notion de paire. Pour désigner un couple, les anglophones emploient d'ailleurs ordered pair, c’est-à-dire paire ordonnée.

Notion de couple

Les objets a et b sont appelés respectivement première composante et deuxième composante du couple ( a, b ).

Propriété caractéristique

D'abord introduite comme une notion primitive, l'essence de la notion de couple réside dans la propriété caractéristique suivante :

Deux couples sont égaux si et seulement si leurs premières composantes d'une part, et leurs secondes composantes d'autre part, sont égales entre elles.

En d'autres termes, quels que soient a₁, a₂, b₁, b₂, on a :

(a₁, a₂) = (b₁, b₂) si et seulement si a₁ = b₁ et a₂ = b₂.

Cette propriété est à comparer avec l'égalité des paires, pour lesquelles b ₁ et b ₂ peuvent être permutés par rapport à a ₁ et a ₂ , ce qui n'est pas le cas pour les couples.

Ceci est confirmé par le corollaire suivant :

Les composantes d'un couple ne peuvent être échangées entre elles sans modifier le couple, sauf si elles sont identiques.

ce que l'on peut exprimer plus formellement par : quels que soient a et b :

( a , b ) = ( b , a ) si et seulement si a = b.

Par conséquent:

• pour un couple ( a , b ) :   b ≠ a ⇒ ( b , a ) ≠ ( a , b )
• pour une paire { a , b } :   { b , a } = { a , b }

^[1]

Les notions de couple et de paire ne doivent donc pas être confondues.

L'ordre des composantes dans un couple a ainsi de l'importance, d'où la définition :

Si a est différent de b , le couple ( b , a ) est appelé couple symétrique ou encore couple réciproque du couple ( a , b ).

Produit cartésien

L'ensemble de tous les couples dont la première composante appartient à un ensemble quelconque X et la seconde à un ensemble quelconque Y est appelé produit cartésien de ces deux ensembles et se note X×Y. Les sous-ensembles de X×Y sont des graphes.

Exemples

• ( 1 , 4 ) et ( 4 , 4 ) sont des couples d'entiers.
• Si E = { 1 , 2 , 3 } alors ( { 1 } , { 1 , 3 } ) et ( Ø , { 1 } ) sont des couples de parties de E.

Les couples en théorie des ensembles

Norbert Wiener fut le premier à remarquer (en 1914) que la notion de couple pouvait se définir en terme d'ensemble, et que donc il n'était pas nécessaire d'introduire cette notion comme une notion primitive, dès que l'on a la notion d'ensemble.

En théorie des ensembles une fonction de couplage est une fonction (au sens intuitif, et non au sens de la théorie des ensembles dans laquelle on travaille) qui à deux objets quelconques x et y, associe un objet noté (x,y) vérifiant la propriété caractéristique des couples. Il existe de nombreuses fonctions de couplages. Habituellement on utilise une repésentation des couples due à Kazimierz Kuratowski (1921). Ce choix est commode, mais n'a rien d'intrinsèque. En particulier toutes les propriétés mathématiques usuelles des couples se déduisent de la propriété caractéristique, le choix de la fonction de couplage ne doit avoir aucune conséquence.

Les couples de Kuratowski

Les couples sont définis en théorie des ensembles de la façon suivante :

Pour x et y deux ensembles quelconques, on pose (x,y)={{x},{x,y}}.

Pour cette définition on doit utiliser trois fois l'axiome de la paire, pour former le singleton {x}, puis pour former la paire (ou singleton) {x,y}, et enfin pour former la paire (ou singleton) {{x},{x,y}}.

On a bien défini la notion de couple de façon unique. On montre ensuite facilement la propriété caractéristique, en utilisant de façon répétée l'axiome d'extensionnalité :

Pour tous ensembles x, y, x' et y' , si {{x},{x,y}}={{x' },{x' ,y' }}, alors x = x' et y = y', ce dans une théorie des ensembles qui vérifie l'axiome de la paire et l'axiome d'extensionalité.

Il suffit d'utiliser la condition d'égalité pour deux paires (ou singletons), en distinguant soigneusement tous les cas possibles.

• Soit {x}={x' } et {x,y}={x' ,y' }. Alors (égalité des deux singletons) x=x' . D'autre part (égalité des deux paires), soit x=x' et y=y' , ce que l'on veut démontrer, soit x=y' et y=x' , mais comme par ailleurs x=x' , les 4 éléments sont égaux d'où le résultat.

• Soit {x}={x' ,y' } et {x,y}={x' }. On déduit de ces deux égalités que les 4 éléments sont égaux d'où le résultat.

Notons ( E) l' ensemble des parties de E. On peut remarquer que si x ∈ X et y ∈ Y alors { x } ∈ ( X ∪ Y ) et { x , y } ∈ ( X ∪ Y ), et donc

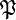
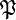
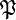
( x , y ) ∈ ( ( X ∪ Y ) )

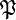
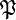
Ceci est utile pour montrer que le produit cartésien de deux ensembles est bien un ensemble (il faut l'axiome de la paire, l'axiome de la réunion, l'axiome de l'ensemble des parties et le schéma d'axiomes de compréhension), en posant Z= ( ( X ∪ Y ) ) :

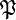
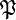
X×Y={z ∈ Z/∃x ∈ X ∃y ∈ Y z=(x,y)}

Réciproquement supposons donné un ensemble de couples C. Alors les composantes de C appartiennent à l'ensemble E obtenu par réunion de la réunion des élements de C, et donc on peut définir les ensembles des premières et des secondes composantes de C par compréhension :

E=∪∪C ; A = {x ∈ E / ∃ y (x,y) ∈ C} ; B = {y ∈ E / ∃ x (x,y) ∈ C}

Ceci est utile pour montrer par exemple que l'ensemble de définition ou l'ensemble image d'une relation ou d'une fonction (vus comme des ensembles de couples) sont bien des ensembles (on utilise l'axiome de la réunion, et le schéma d'axiomes de compréhension).

D'autres fonctions de couplage

Wiener, en 1914, utilisait la définition suivante des couples : (x,y)={ {{x},∅}, { {y} } }, qui est à peine plus compliquée que celle de Kuratowski.

On peut aussi utiliser (x,y)={x,{x,y}} mais la preuve de la propriété caractéristique demande l'axiome de fondation !

Généralisations

Les triplets peut être défini comme vérifiant la propriété caractéristique :

deux triplets sont égaux si et seulement si leurs premières composantes sont égales entre elles, leurs deuxièmes composantes aussi et leurs troisièmes composantes de même.

Un triplet ( a , b , c ) peut être codé comme ( a , ( b , c ) ) soit deux couples imbriqués. Le choix de l'ordre d'imbrication est purement arbitraire. On peut généraliser le procédé de construction à des n-uplets, n étant un entier quelconque. Pour généraliser à une infinité de composantes, on ne parle plus de uples, mais de fonction, de suite éventuellement dans le cas dénombrable.

Les généralisations à plus de deux composantes sont étudiées en détail dans l'article " Produit cartésien "