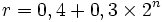Loi de Titius-Bode - Définition
La loi de Titius-Bode, ou loi de Bode, est une règle empirique reliant les rayons des orbites des planètes du système solaire. Elle montre que la distance des planètes au Soleil suit une progression géométrique de raison 1,75. Mise en évidence par le mathématicien Max Wolf dès 1741, elle a été redécouverte et formalisée mathématiquement en 1766 par Johann Daniel Tietz, dit Titius. Mais c'est à Johann Elert Bode qu'est longtemps revenue la paternité de cette loi en la faisant connaître auprès de la communauté des astronomes en 1778.
Récemment, on a cherché à intègrer les nouveaux corps découverts dans la suite de Titus-Bode, sans savoir s'ils seraient finalement considèrés comme des planètes. Aujourd'hui, les objets ayant les plus hauts numéros dans la suite de Titus-Bode ne sont pas considèrés comme des planètes.
Expression mathématique
La loi de Titius-Bode permet de calculer une approximation du rayon r de l'orbite d'une planète en fonction de son rang n, à partir de la formule :
- où r est exprimé en unité astronomique (UA)
- et n vaut -∞ pour Mercure, 0 pour Vénus, 1 pour la Terre, 2 pour Mars, 3 pour la ceinture d' astéroïdes, etc.
Une autre expression de cette loi consiste à partir de la suite de nombre : 0, 3, 6, 12 ... (qui s'apparente à la suite géométrique un+1 = 2*un). Á chaque nombre (0 pour Mercure, 3 pour Vénus, etc.) on ajoute 4, puis on divise la somme par 10. Le résultat de l'opération est le même que l'expression mathématique de Titius, il donne une valeur approchée de la distance Soleil-planète en UA. Cette loi de répartition a été améliorée par Otto Schmidt en appliquant une fonction pour les planètes telluriques et une autre pour les planètes gazeuses.
Découverte de la ceinture d'astéroïdes
| Planète | n | Distance calculée |
Distance réelle |
Erreur absolue |
Erreur relative |
|---|---|---|---|---|---|
| Mercure | -∞ | 0,4 | 0,39 | 0,01 | 2,6% |
| Vénus | 0 | 0,7 | 0,72 | 0,02 | 2,8% |
| Terre | 1 | 1,0 | 1,00 | 0 | 0% |
| Mars | 2 | 1,6 | 1,52 | 0,08 | 5,3% |
| Cérès | 3 | 2,8 | 2,77 | 0,03 | 1,1% |
| Jupiter | 4 | 5,2 | 5,20 | 0 | 0% |
| Saturne | 5 | 10,0 | 9,54 | 0,46 | 4,8% |
| Uranus | 6 | 19,6 | 19,2 | 0,4 | 2,1% |
| Neptune | - | - | 30,1 | - | - |
| Pluton | 7 | 38,8 | 39,5 | 0,7 | 1,8% |
| Sedna | 8 | 77,2 | 76,1 [1] | 1,2 | 1,6% |
Lors de sa publication originale, la loi était vérifiée par toutes les planètes connues, de Mercure à Saturne, avec une lacune entre les quatrième (n = 2) et cinquième (n = 4) planètes. Cette loi était alors considérée comme intéressante mais sans grande importance. La découverte d'Uranus dont l'orbite respecte la loi, la validera aux yeux d'une grande partie de la communauté scientifique. Mettant à profit cette nouvelle crédibilité, Bode poussera à la recherche de la planète intermédiaire manquante (n = 3), ce qui conduira à la découverte de Cérès, le plus grand des astéroïdes.
Urbain Le Verrier et John Couch Adams utiliseront ensuite cette loi pour prévoir l'orbite d'une nouvelle planète Neptune qui pourrait expliquer les perturbations d'Uranus. Cette valeur de 38,8 est assez mauvaise et correspond plutôt à l'orbite de Pluton.
Pour expliquer cette exception (Neptune), il a été suggéré que quelque chose avait altéré l'orbite des trois planètes externes du système solaire, peut être le passage d'une masse volumineuse comme celle de l'hypothèse de Némésis.
Les dernières théories expliquent la loi de Titius-Bode comme la conséquence de mécanismes de résonance qui créeraient des zones orbitales stables lors de la création des systèmes solaires.
Variante
Dans le même esprit on peut remarquer que la distribution des planètes suit plus une moins une loi logarithmique.
On obtient le même genre d'alignement avec les satellites galiléens de Jupiter.
Remarque: On a proportionalité, c'est-à-dire une droite passant par l'origine, en donnant à mercure le numéro 7.
| Ordre | Planète | Distance au Soleil (UA) | Valeur (ln) |
|---|---|---|---|
| -∞ | Mercure | 0,38 | -0,97 |
| 0 | Vénus | 0,72 | -0,33 |
| 1 | Terre | 1,00 | 0,00 |
| 2 | Mars | 1,52 | 0,42 |
| 3 | (1) Cérès | 2,77 | 1,02 |
| 4 | Jupiter | 5,20 | 1,65 |
| 5 | Saturne | 9,54 | 2,26 |
| 6 | Uranus | 19,2 | 2,95 |
| 7 | Pluton | 39,5 | 3,68 |
| 8 | Sedna | 76,1 | 4,33 |