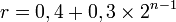Loi de Titius-Bode - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La loi de Titius-Bode, souvent appelée loi de Bode, est une relation empirique entre les rayons des orbites des planètes du système solaire, qui utilise une suite arithmético-géométrique de raison 2.
Elle a été énoncée en 1766 par Johann Daniel Tietz, alias Titius, qui avait trouvé une relation numérique dans les termes de la suite des distances des planètes, citées en 1724 par le philosophe Christian Wolff (et non par l'astronome Max Wolf, qui n'était pas encore né). Wolff n'avait d'ailleurs fait que recopier la suite des nombres 4, 7, 10, 15, 52, 95, mentionnée en 1702 par James Gregory, qui représentait les distances des planètes en 1/10 du rayon de l'orbite terrestre. Mais c'est à Johann Elert Bode qu'est longtemps revenue la paternité de cette "loi", qu'il avait publié en 1772 dans Deutliche Anleitung zur Kenntniß des gestirnten Himmels.
Validée en 1781 par la découverte d'Uranus, la "loi de Bode" a été mise en échec en 1846 par la découverte de Neptune, et ne donne plus de résultats probants au-delà.
Expression mathématique
L'expression d'origine était faite en exprimant les distances en dixièmes de la distante Terre-Soleil (l'unité astronomique, UA). Les distances supposées sont :
- pour Mercure : 4
- pour Vénus : 4 + 3
- pour la Terre : 4 + 3×2
- pour Mars : 4 + 3×4
- etc.
En termes plus mathématiques, la formule à utiliser pour trouver la distance de la planète au Soleil est :
- où r est exprimé en UA
- n est le "rang" de la planète
Il s'agit d'une suite arithmético-géométrique.
n vaut -∞ (moins l'infini) pour Mercure, 1 pour Vénus, 2 pour la Terre, 3 pour Mars, 4 pour la ceinture d'astéroïdes, etc.
On peut jouer sur des variantes d'écriture, par exemple écrire
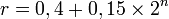
Faiblesses intrinsèques
La première faiblesse de cette loi est l'utilisation de -∞ comme rang pour Mercure, qui brise le caractère arithmético-géométrique de la suite. La seule raison de ce -∞ est de faire mieux correspondre la loi à la réalité.
La seconde faiblesse est que quand la loi fut formulée, le rang 4 semblait inoccupé ; la découverte de la ceinture d'astéroïdes sembla conforter la loi, mais on peut critiquer le fait d'intégrer à cette loi la ceinture alors que tous les astéroïdes réunis n'ont pas la masse d'une planète. Si l'on cherche à donner une explication, il faut alors aussi expliquer pourquoi cette ceinture prend la place d'une planète.
Enfin, il n'a jamais été précisé ce que signifie « rayon » ou « distance » dans l'énoncé de la loi. En effet, pour que ces notions soient clairement définies, il faudrait que les orbites soient parfaitement circulaires. C'est loin d'être le cas des planètes à proprement parler (Mercure en particulier, dont la distance au Soleil varie d'un facteur 1,5) et certains objets qu'on tenta d'ajouter à la progression l'étaient encore moins. Généralement, on retient le demi-grand axe comme distance.
| Planète | Loi de Titius-Bode | Valeurs réelles | Erreur | |||||
|---|---|---|---|---|---|---|---|---|
| Rang attribué | Distance prédite | Demi-grand axe | Périphélie | Aphélie | Excentricité | absolue | relative | |
| Mercure | -∞ | 0,4 | 0,387 | 0,307 | 0,467 | 0,206 | 0,013 | 3,4% |
| Vénus | 1 | 0,7 | 0,723 | 0,718 | 0,728 | 0,007 | 0,023 | 3,2% |
| Terre | 2 | 1,0 | 1,000 | 0,983 | 1,017 | 0,017 | 0,000 | 0,0% |
| Mars | 3 | 1,6 | 1,523 | 1,381 | 1,665 | 0,093 | 0,077 | 5,1% |
| Cérès | 4 | 2,8 | 2,765 | 2,547 | 2,983 | 0,079 | 0,035 | 1,3% |
| Jupiter | 5 | 5,2 | 5,203 | 4,953 | 5,453 | 0,048 | 0,003 | 0,1% |
| Saturne | 6 | 10,0 | 9,537 | 9,022 | 10,052 | 0,054 | 0,463 | 4,9% |
| Uranus | 7 | 19,6 | 19,229 | 18,325 | 20,133 | 0,047 | 0,371 | 1,9% |
| Neptune | 8 | 38,8 | 30,069 | 29,798 | 30,340 | 0,009 | 8,731 | 29,0% |