2 (nombre) - Définition

Introduction

2 (deux) est l'entier naturel suivant 1 et précédant 3.

Évolution du glyphe

Le glyphe que nous utilisons aujourd'hui dans le monde occidental pour représenter le nombre 2 trouve ses racines chez les brahmanes hindous, qui écrivaient 2 sous forme de deux lignes horizontales (il est encore écrit de cette manière dans la Chine moderne, et est analogue au chiffre romain II). Les Gupta ont tourné les deux lignes à 45 degrés, pour en faire des diagonales. Ils ont aussi fait quelquefois une petite ligne au sommet et une fin incurvée à la base vers le centre de la ligne du bas. Apparemment pour aller plus vite, les Nagari ont démarré la ligne du haut plus incurvée et l'ont connecté à la ligne du bas. Les arabes Ghubar ont fait la ligne du bas complètement verticale, le glyphe ressemblait à un point d'interrogation sans point. En restaurant la ligne du bas dans sa position horizontale originale, mais en gardant la ligne du haut sous sa forme de courbe qui se connecte à cette première ligne cela nous conduit à notre glyphe moderne.

En mathématiques

Deux possède beaucoup de propriétés en mathématiques. Un entier est appelé pair s'il est divisible par 2, c’est-à-dire sans reste. Sinon, il est qualifié d'impair. Pour les entiers écrits dans un système de numération basé sur un nombre pair, tel que les systèmes décimal et hexadécimal, la divisibilité par 2 est facilement testée par un examen simple du dernier chiffre. S'il est pair, alors le nombre total est pair.

Deux est le plus petit et le premier nombre premier, et le seul pair. Malgré sa primalité, deux est aussi un nombre hautement composé, car il possède plus de diviseurs que un. Le nombre hautement composé suivant est 4.

Deux est un nombre intouchable.

Deux est un nombre premier super-singulier.

Deux est un facteur de 10, donc les fractions avec 2 dans le dénominateur ne donneront pas de développement décimal infini, comme c'est le cas avec la plupart des nombres premiers.

Quand on multiplie un nombre par 2, on a le double du nombre de départ. Quand on divise un nombre par 2, on a la moitié du nombre de départ.

Deux est la base du système de numération le plus simple dans lequel les nombres naturels peuvent être écrits de manière concise, le système binaire est largement utilisé dans les ordinateurs.

Pour tout nombre x :

 : de l'addition à la multiplication,

 : de la multiplication à l'exponentiation,

 : de l'exponentiation aux puissances itérées de Knuth.

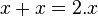
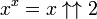
Les puissances de 2 sont centrales dans le concept des nombres premiers de Mersenne, et importants en informatique. 2 est le premier nombre premier de Mersenne mis en exposant.

Extraire une racine carrée d'un nombre est une opération mathématique tellement banale, que la place du signe de la racine où est placé l'exposant (par exemple 3 pour la racine cubique de x : ) est laissée blanche pour les racines carrées (exemple : ), considérée comme tacite.

La racine carrée de 2 a été le premier nombre irrationnel connu par les pythagoriciens.

Le plus petit corps possède deux éléments.

Dans la construction théorique de l'ensemble des nombres naturels, 2 est identifié avec l'ensemble {0,1}. Ce dernier ensemble est important dans la théorie des catégories : c'est un classificateur de sous-objet dans la catégorie des ensembles.

Deux est une primorielle, en tant que sa propre factorielle. Deux apparait souvent dans des suites numériques, telles que les suites de Fibonacci, mais pas aussi souvent que un. Deux est aussi un nombre de Motzkin, le premier nombre premier de Sophie Germain, un nombre de Bell, un nombre Harshad complet, un nombre oblong, un nombre méandrique, un nombre semi-méandrique et un nombre méandrique ouvert.

Deux est le nombre de solutions du problème des n-dames pour n = 4.

Dans un polyèdre, on a toujours la relation suivante, qu'on peut démontrer : (où f représente le nombre de faces, s le nombre de sommets et a le nombre d'arêtes). C'est la relation d'Euler. On obtient le même résultat en effectuant l'opération similaire en dimension 5, 7, 9 etc.