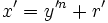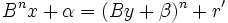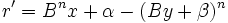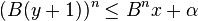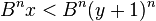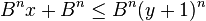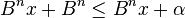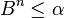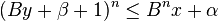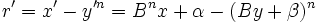Algorithme de décalage n-racines - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'algorithme de décalage n-racines est un algorithme pour extraire la ne racine d'un nombre réel. Itératif, il procède en décalant n chiffres du radicande à partir du chiffre le plus significatif. Ressemblant à la division au long, il retourne un chiffre à chaque itération.
Description
Notation
Posons B la base du système de nombres et n le degré de la racine à extraire. Soit x le radicande à traiter, y la racine extraite jusqu'à maintenant et r le reste. Soit α les prochains n chiffres du radicande, et β le prochain chiffre de la racine. Soit x' la nouvelle valeur de x dans la prochaine itération, y' la nouvelle valeur de y dans la prochaine itération et r' la nouvelle valeur de r dans la prochaine itération. Ces trois nombres sont entiers.
Invariants
À chaque itération, l'invariant
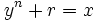
 sera vrai. Alors, y est le plus grand entier plus petit que la ne racine de x et r est le reste.
sera vrai. Alors, y est le plus grand entier plus petit que la ne racine de x et r est le reste.
Initialisation
Les valeurs initiales de x, y et r sont 0. Pour la première itération, la valeur d'α devrait être le bloc le plus significatif de n chiffres du radicande. Noter que l'alignement se fait à partir de la virgule décimale. Par exemple, dans 123,4 le bloc le plus significatif de 2 chiffres est 01, le prochain est 23 et le troisième est 40.
Boucle principale
À chaque itération, décaler n chiffres du radicande, de façon à avoir
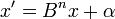
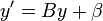
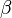
Le premier invariant est :
ou
Choisir le plus grand
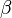
et poser
Un tel
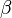
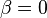
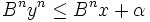
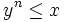
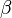
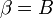
mais le deuxième invariant implique que
et puisque
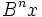
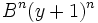
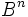
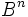
et
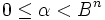
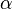
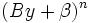
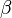
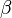
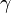
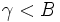
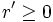
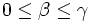
Considérons le deuxième invariant:
ou
Si
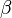
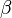
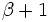
Ceci viole le premier invariant. pour satisfaire les deux invariants, il faut choisir le plus grand
L'existence et l'unicité de
En résumé, à chaque itération :
- Soit
- Soit
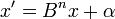
- Soit
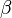
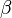
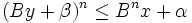
- Soit
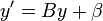
- Soit
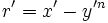
En notant que
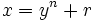
est équivalente à
et
est équivalente à
Donc, x est superflu et puisque
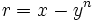
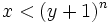
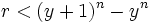
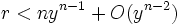
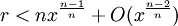
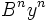
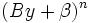
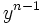
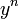
La forme finale de l'algorithme est :
- Initialiser r and y to 0
- Répéter jusqu'à la précision désirée :
- Soit α le prochain bloc de chiffres du radicande
- Soit
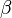
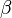
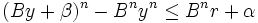
- Soit y' = By + β
- Soit
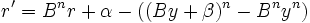
- Assigner
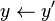
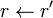
- y est le plus grand entier tel que
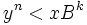
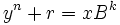
Les ne racines avec papier crayon
Tel qu'indiqué plus haut, cet algorithme ressemble à la longue division et sa notation est semblable :
Note : la notation utilisée est courante dans le monde anglo-saxon. La valeur de la racine apparaît au-dessus du symbole de la racine.
1. 4 4 2 2 4 ---------------------- 3/ 3.000 000 000 000 000 /\/ 1 = 300*(0^2)*1+30*0*(1^2)+1^3 - 2 000 1 744 = 300*(1^2)*4+30*1*(4^2)+4^3 ----- 256 000 241 984 = 300*(14^2)*4+30*14*(4^2)+4^3 ------- 14 016 000 12 458 888 = 300*(144^2)*2+30*144*(2^2)+2^3 ---------- 1 557 112 000 1 247 791 448 = 300*(1442^2)*2+30*1442*(2^2)+2^3 ------------- 309 320 552 000 249 599 823 424 = 300*(14422^2)*4+30*14422*(4^2)+4^3 --------------- 59 720 728 576
Après une ou deux itérations, le premier terme domine dans (By + β)n − Bnyn, alors nous pouvons obtenir une première estimation de β en divisant Br + α par nBn − 1yn − 1.
Performance
À chaque itération, la tâche qui consomme le plus de temps est le choix de β. Ayant B valeurs possibles, il est possible de trouver β en effectuant O(log(B)) comparaisons. Chacune exige d'évaluer (By + β)n − Bnyn. À la ke itération, y possède k chiffres, et le polynôme peut être évalué en faisant 2n − 4 multiplications d'au plus k(n − 1) chiffres et n − 2 additions d'au plus k(n − 1) chiffres, une fois connues les puissances de y et β jusqu'à n − 1 pour y et n de β. Par ailleurs, les valeurs de β sont peu nombreuses, il est donc possible d'obtenir β dans un temps constant. Les puissances de y peuvent être calculées n − 2 multiplications d'au plus k(n − 1) chiffres. En faisant l'hypothèse qu'une multiplication de n chiffres prend O(n2) et l'addition prend O(n), alors il en coûte O(k2n2) à chaque comparaison, ou O(k2n2log(B)), pour choisir β. La portion restante de l'algorithme demande des additions et des soustractions consommant O(k). Donc, chaque itération prend O(k2n2log(B)). Pour k chiffres, il faut compter O(k3n2log(B)).
La seule mémoire interne nécessaire est r, qui contient O(k) chiffres après la ke itération. Cet algorithme n'ayant pas de limite supérieure sur la mémoire impose une limite supérieure sur le nombre de chiffres que l'on peut calculer de tête, au contraire des algorithmes arithmétiques plus élémentaires. Malheureusement, n'importe quelle machine à états finis avec un intrant périodique ne peut que retourner un extrant périodique. Il n'existe donc pas d'algorithme capable de calculer un nombre irrationnel à partir d'un nombre rationnel. En conséquence, il n'existe pas d'algorithme capable de calculer une racine à l'intérieur d'une mémoire limitée.
Plus la base est grande, plus le temps pour choisir β est grand par un facteur O(log(B)), mais, en même temps, diminue le nombre de chiffres nécessaires pour atteindre la même précision par le même facteur. Puisque l'algorithme est propotionnel au cube du nombre de chiffres, augmenter la base augmente la vitesse d'exécution par le facteur O(log2(B)).
Cependant, lorsque la base est plus grande que le radicande, l'algorithme dégenère en une dichotomie. À ce moment, il est inutile puisque la dichotomie est plus efficace.