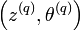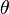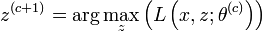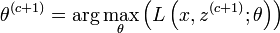Algorithme espérance-maximisation - Définition
La liste des auteurs de cet article est disponible ici.
Principe de fonctionnement
En considérant un échantillon
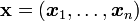
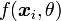
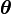
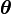
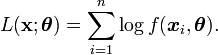
Cet algorithme est particulièrement utile lorsque la maximisation de L est très complexe mais que, sous réserve de connaître certaines données judicieusement choisies, on peut très simplement déterminer
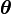
Dans ce cas, on s'appuie sur des données complétées par un vecteur
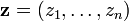
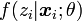
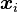
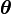
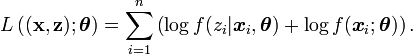
et donc,
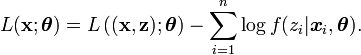
L'algorithme EM est une procédure itérative basée sur l'espérance des données complétées conditionnellement au paramètre courant. En notant
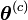
![E\left[L(\mathbf{x};\boldsymbol{\theta})|\boldsymbol{\theta}^{(c)}\right]=E\left[L\left(\mathbf{(x,z)};\boldsymbol{\theta}\right))|\boldsymbol{\theta}^{(c)}\right]-E\left[\sum_{i=1}^n\log f(z_i|\boldsymbol{x}_i,\boldsymbol{\theta}))|\boldsymbol{\theta}^{(c)}\right],](https://static.techno-science.net/illustration/Definitions/autres/9/9535ef81a8157f8d9e4b8af81bea0d1c_e5f1f35f0b64c3af3935a0e0cc66dfda.png)
ou encore
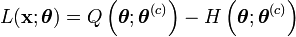
avec
![Q\left(\boldsymbol{\theta};\boldsymbol{\theta}^{(c)}\right)=E\left[L\left(\mathbf{(x,z)};\boldsymbol{\theta}\right))|\boldsymbol{\theta}^{(c)}\right]](https://static.techno-science.net/illustration/Definitions/autres/3/38f8b92ae34438b9c8fb9552037b6fdb_a7600f005de694040da19ecb06531b64.png)
![H\left(\boldsymbol{\theta};\boldsymbol{\theta}^{(c)}\right)=E\left[\sum_{i=1}^n\log f(z_i|\boldsymbol{x}_i,\boldsymbol{\theta}))|\boldsymbol{\theta}^{(c)}\right]](https://static.techno-science.net/illustration/Definitions/autres/3/3fe5f7864f12cd9db840f88ea740db47_e293ab699ac754ffcea28740f084bd4b.png)
On montre que la suite définie par
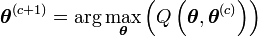
fait tendre
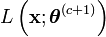
On peut donc définir l'algorithme EM de la manière suivante:
- Initialisation au hasard de
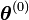
- c=0
- Tant que l'algorithme n'a pas convergé, faire
-
- Evaluation de l'espérance (étape E) :
![Q\left(\boldsymbol{\theta};\boldsymbol{\theta}^{(c)}\right)=E\left[L\left(\mathbf{(x,z)};\boldsymbol{\theta}\right))|\boldsymbol{\theta}^{(c)}\right]](https://static.techno-science.net/illustration/Definitions/autres/3/38f8b92ae34438b9c8fb9552037b6fdb_a7600f005de694040da19ecb06531b64.png)
- Maximisation (étape M) :
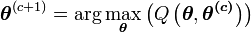
- c=c+1
- Evaluation de l'espérance (étape E) :
- Fin
En pratique, pour s'affranchir du caractère local du maximum atteint, on fait tourner l'algorithme EM un grand nombre de fois à partir de valeurs initiales différentes de manière à avoir de plus grandes chances d'atteindre le maximum global de vraisemblance.
Variantes usuelles d'EM
L'algorithme EM allie, dans la plupart des cas, simplicité de mise en oeuvre et efficacité. Néanmoins quelques cas problèmatiques ont donné lieu à des développements complémentaires. Parmi les variantes existantes de cet algorithme nous évoquerons l'algorithme GEM (Generalized EM) qui permet de simplifier le problème de l'étape maximisation; l'algorithme CEM (Classification EM) permettant de prendre en compte l'aspect classification lors de l'estimation, ainsi que l'algorithme SEM (Stochastic EM) dont l'objectif est de réduire le risque de tomber dans un optimum local de vraisemblance.
Algorithme GEM
GEM a été proposé en même temps qu'EM par Dempster et al. (1977) qui ont prouvé que pour assurer la convergence vers un maximum local de vraisemblance, il n'est pas nécessaire de maximiser Q à chaque étape mais qu'une simple amélioration de Q est suffisante.
GEM peut donc s'écrire de la manière suivante:
- Initialisation au hasard de
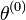
-
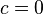
- Tant que l'algorithme n'a pas convergé, faire
-
- choisir
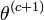

-
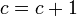
- choisir
- Fin
Algorithme CEM
L'algorithme EM se positionne dans une optique estimation, c'est-à-dire qu'on cherche à maximiser la vraisemblance du paramètre
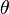
L'approche classification, proposée par Celeux et Govaert (1991) consiste à optimiser, non pas la vraisemblance du paramètre, mais directement la vraisemblance complétée, donnée, dans le cas des modèles de mélange, par
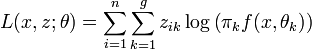
Pour cela, il suffit de procéder de la manière suivante:
- Initialisation au hasard de
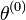
-
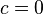
- Tant que l'algorithme n'a pas convergé, faire
- Fin
Algorithme SEM
Afin de réduire le risque de tomber dans un maximum local de vraisemblance, Celeux et Diebolt (1985) proposent d’intercaler une étape stochastique de classification entre les étapes E et M. Après le calcul des probabilités
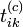
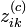
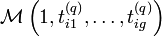
Contrairement à ce qui se produit dans l’algorithme CEM, on ne peut considérer que l’algorithme a convergé lorsque les individus ne changent plus de classes. En effet, celles-ci étant tirées aléatoirement, la suite