Algorithme évolutionniste - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les algorithmes évolutionnistes ou algorithmes évolutionnaires (evolutionary computation en anglais), sont une famille d'algorithmes s'inspirant de la théorie de l'évolution pour résoudre des problèmes divers. Ils font ainsi évoluer un ensemble de solutions à un problème donné, dans l'optique de trouver les meilleurs résultats. Ce sont des algorithmes stochastiques, car ils utilisent itérativement des processus aléatoires.
La grande majorité de ces méthodes sont utilisées pour résoudre des problèmes d'optimisation, elles sont en cela des métaheuristiques, bien que le cadre général ne soit pas nécessairement dédié aux algorithmes d'optimisation au sens strict. On les classe également parmi les méthodes d'intelligence calculatoire (Computational intelligence en anglais).
Paradigme
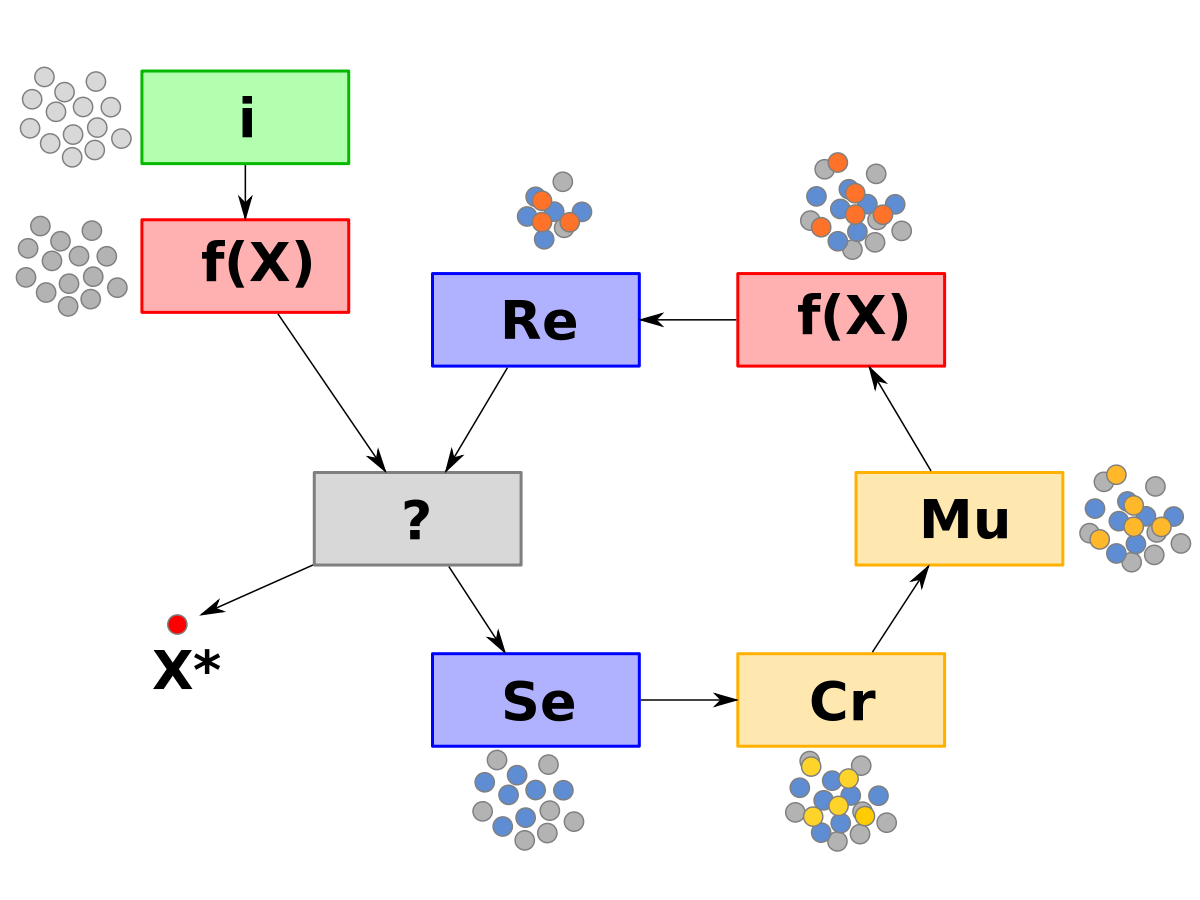
Ces algorithmes manipulent des populations de solutions.
Les algorithmes évolutionnaires s'inspirent de l'évolution des êtres vivants, en considérant que celle-ci tend à produire des organismes plus adaptés à leur environnement.
Selon la théorie de l'évolution, plusieurs mécanismes sont à l'œuvre pour ce faire. Schématiquement :
- Les caractéristiques d'un organisme sont en grande partie codées dans ses gènes,
- chaque population d'organismes est composée d'individus tous différents,
- les différences entre individus leur confèrent une adaptation plus ou moins grande à leur environnement,
- les organismes transmettent une partie de leurs caractéristiques à leurs descendants,
- les individus les plus adaptés se reproduisent plus « efficacement », leurs caractéristiques ont donc tendance à davantage se répandre dans la population.
Principales familles
Historiquement, trois grandes familles d'algorithmes ont été développées indépendamment, entre la moitié des années 1960 et 70. Les premières méthodes furent les stratégies d'évolution, proposées par I. Rechenberg en 1965, pour résoudre des problèmes d'optimisations continus. L'année suivante, Fogel, Owens et Walsh concoivent la programmation évolutionnaire comme une méthode d'intelligence artificielle pour la conception d'automates à états finis. Enfin, en 1975, J. H. Holland propose les premiers algorithmes génétiques, pour l'optimisation combinatoire. La parution en 1989 du livre de D. E. Goldberg sur les algorithmes génétiques rendra ceux-ci particulièrements populaires.
Par la suite, ces différentes approches ont beaucoup évoluées et se sont rapprochées, pour finir par êtres regroupées sous le terme générique d'algorithmes évolutionnaires. Aujourd'hui, la littérature sur le sujet est extrêmement abondante, et ces algorithmes sont considérés comme un domaine de recherche très prolifique.
Stratégies d'évolution
Dans sa version de base, l'algorithme manipule itérativement un ensemble de vecteurs de variables réelles, à l'aide d'opérateurs de mutation et de sélection. La sélection s'effectue par un choix déterministe des meilleurs individus, selon l'échelle de valeur de la fonction objectif. L'étape de mutation est classiquement effectuée par l'ajout d'une valeur aléatoire, tirée au sein d'une distribution normale. Une particularité caractéristique de ces algorithmes est l'auto-adaptation de la matrice de variance-covariance de la distribution normale.
Un algorithme représentatif des stratégies d'évolution est l'évolution différentielle. Dans cette classe de méthode, on utilise la différence pondérée entre sous-populations pour biaiser un opérateur de mutation différentiel.
Programmation évolutionnaire
Historiquement, ces algorithmes étaient conçus pour des problèmes d'apprentissage à partir d'automates à états finis et n'utilisaient que des opérateurs de mutation et de remplacement. Cependant, aujourd'hui ils ne se limitent plus à une représentation, mais n'utilisent toujours pas d'opérateur de croisement. Ils diffèrent des stratégies d'évolution en ce qu'ils privilégient des opérateurs de remplacement stochastiques.
Algorithmes génétiques
Les algorithmes génétiques sont les plus populaires des algorithmes évolutionnaires. Ils différencient explicitement le génotype du phénotype, le génotype étant généralement codé de façon binaire. Le choix du codage du génotype (la façon dont il est relié au phénotype) est crucial pour un algorithme génétique. Classiquement, ils utilisent un opérateur de sélection proportionnel, un remplacement générationnel et l'opérateur de croisement est l'opérateur principal.
Des algorithmes évolutionnaires utilisant d'autres représentations et opérateurs sont souvent appelés algorithmes génétiques, bien que les spécialistes évitent cet abus de langage.
Programmation génétique
Ces algorithmes utilisent une représentation en arbres d'expressions logiques, du fait qu'ils sont historiquement appliqués à l'apprentissage statistique et la modélisation. Ils utilisent pour ce faire le même algorithme de base que les algorithmes génétiques. Cependant, la programmation génétique s'intéresse spécifiquement à la construction automatique de programmes.
Algorithmes à estimation de distribution
Contrairement aux algorithmes évolutionnaires « classiques », le cœur de ces méthodes consiste à estimer les relations entre les différentes variables d'un problème d'optimisation, grâce à l'estimation d'une distribution de probabilité, associée à chaque point de l'échantillon. Ils n'emploient donc pas d'opérateurs de croisement ou de mutation, l'échantillon étant directement construit à partir des paramètres de distribution, estimés à l'itération précédente.