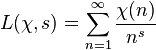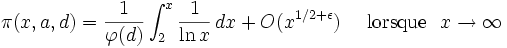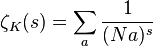Hypothèse de Riemann généralisée - Définition
L'hypothèse de Riemann est l'une des plus importantes conjectures des mathématiques et concerne les zéros de la fonction ζ de Riemann. Divers objets géométriques et arithmétiques peuvent être décrits par ce que l'on appelle les fonctions L globales, qui sont similaires formellement à la fonction Zeta de Riemann. On peut alors se poser la même question à propos des zéros de ces fonctions L, fournissant diverses généralisations de l'hypothèse de Riemann. Aucune de ces conjectures n'a été confirmée ou infirmée par une démonstration, mais beaucoup de mathématiciens croient qu'elles sont vraies.
Les fonctions L globales peuvent être associées aux courbes elliptiques, aux corps de nombres (dans ce cas, elles sont appelées fonction Zeta de Dedekind), ondes de Maass, et caractères de Dirichlet (dans ce cas, elles sont appelées fonctions L de Dirichlet). Lorsque l'hypothèse de Riemann est formulée pour les fonctions Zeta de Dedekind, elle est connue sous le nom d'hypothèse de Riemann étendue et lorsqu'elle est formulée pour les fonctions L de Dirichlet, elle est connue sous le nom d'hypothèse généralisée de Riemann. Ces deux énoncés seront discutés de façon plus détaillée ci-dessous.
Hypothèse de Riemann généralisée (HRG)
L'hypothèse de Riemann généralisée a sans doute été formulée pour la première fois par Plitz en 1884. De même que l'hypothèse de Riemann originelle, elle a d'importantes conséquences sur la répartition des nombres premiers.
Son énoncé formel est le suivant :
Un caractère de Dirichlet est une fonction arithmétique complètement multiplicative χ pour laquelle il existe un entier strictement positif k tel que, pour tout entier n, on ait
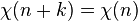
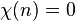
Si on se donne un tel caractère, on définit la fonction L de Dirichlet correspondante par la relation suivante :
pour tout nombre complexe s de partie réelle > 1. Par prolongement analytique, cette fonction peut-être étendue à une fonction méromorphe définie sur tout le plan complexe.
D'après l'hypothèse de Riemann généralisée, pour tout caractère de Dirichlet χ et tout nombre complexe s avec
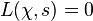
Le cas χ(n) = 1 pour tout n correspond à l'hypothèse de Riemann ordinaire.
Conséquences de l'hypothèse de Riemann généralisée
Un progression arithmétique d'entiers naturels est une suite d'entiers de la forme a, a+d, a+2d, a+3d... où a et d sont des entiers, d étant non nul. D'après le théorème de Dirichlet, si a et d sont premiers entre eux, alors une telle progression arithmétique contient une infinité de nombres premiers.
Notons π(x,a,d) le nombre de nombres premiers appartenant à cette progression et inférieurs ou égaux à x ; si l'hypothèse de Riemann généralisée est vraie, alors pour tous entiers premiers entre eux a et d et pour tout réel ε > 0 :
où
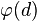
Si l'hypothèse de Riemann généralisée est vraie, alors pour tout nombre premier p, il existe une racine primitive modulo p (un générateur du groupe multiplicatif des entiers modulo p) qui est inférieur à 70 (ln(p))2 ; ce résultat est souvent utilisé dans les démonstrations.
La conjecture faible de Goldbach découle aussi de l'hypothèse de Riemann généralisée.
Si l'hypothèse de Riemann généralisée est vraie, alors le test de primalité de Miller-Rabin est assuré d'être exécuté en temps polynomial. Un test de primalité en temps polynomial qui ne requiert pas l'hypothèse de Riemann généralisée a été récemment publié :
Hypothèse de Riemann étendue (HRE)
Supposons




pour chaque nombre complexe s avec une partie réelle > 1. La somme s'étend sur tous les idéaux différents de l'idéal zéro a de OK.
La fonction Zeta de Dedekind satisfait une équation fonctionnelle et peut être étendue par prolongement analytique sur le plan complexe entier. La fonction résultante contient une information importante à propos du corps de nombres K. L'hypothèse de Riemann étendue affirme que pour chaque corps de nombres K et pour chaque nombre complexe s avec ζK(s) = 0: si la partie réelle de s est comprise entre 0 et 1, alors elle est en fait 1/2.
L'hypothèse ordinaire de Riemann découle de l'hypothèse étendue, si le corps de nombres est