Caractère de Dirichlet - Définition

Propriétés

Propriétés élémentaires

• Les valeurs non nulles du caractère sont des racines φ(n)^èmes de l'unité si φ désigne l'indicatrice d'Euler.

En effet, l'ordre du groupes des unités de Z/nZ est égal à φ(n), le théorème de Lagrange sur les groupes permet de conclure.

• Le produit de deux caractères est un caractère.

• Si χ est un caractère, alors le conjugué de χ est aussi un caractère, il correspond à son caractère inverse pour la multiplication.

• L'image de l'inverse d'un élément du groupe des unités de Z/nZ par un caractère de Dirichlet est le conjugué de son image.

Ces différentes propriétés montrent que l'ensemble des caractères de conducteur n forme un groupe abélien.

Analyse harmonique

• Les caractères de Dirichlet de conducteur n forment un groupe isomorphe au groupe des unités U de Z/nZ.

Cette propriété est le propre de l'ensemble des caractères de tout groupe abélien fini. Elle est démontrée dans le paragraphe Groupe abélien de l'article Caractère d'un groupe fini.

Ici C^U désigne l'ensemble des fonctions du groupe des unités à valeurs complexes. C'est un espace vectoriel complexe. Il peut être muni du produit hermitien noté ici < , > et défini par :

Ici le conjugué d'un nombre complexe c est noté c^*.

• L'ensemble des caractères de Dirichlet forme une base orthonormale de C^U.

Cette propriété est aussi générale à tout groupe de caractères d'un groupe abélien fini, elle est démontrée dans le paragraphe Algèbre du groupe de l'article Caractère d'un groupe fini.

La transformée de Fourier d'une fonction f de C^U est définie, c'est une fonction notée ici de l'ensemble des caractères, noté ici et à valeurs dans les complexes. Elle vérifie la formule suivante :

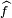
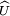
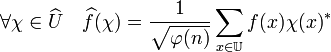
La théorème de Plancherel exprime l'égalité suivante :

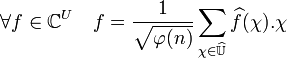
Symbole de Legendre

• Si n est plus grand que deux, alors l'ordre du groupe des unités est pair.

En effet, si p est un nombre premier diviseur de n différent de deux alors p - 1 est un diviseur de φ(n) et p - 1 est pair. Sinon n est égal à 2^r où r est un entier strictement supérieur à 1 et φ(n) est égal à 2^{r - 1}.

• Si n est une puissance d'un nombre premier impair alors il existe un unique caractère non principal à valeurs réelles, c'est le symbole de Legendre.

En effet, si le conducteur est une puissance d'un nombre premier impair, alors le groupe des unités est cyclique (cf le paragraphe Cas où n n'est pas premier de l'article Anneau Z/nZ). L'ordre du groupe multiplicatif est pair, il existe donc un unique élément d'ordre deux. Le groupe des caractères, isomorphe au groupe multiplicatif ne contient lui aussi qu'un élément d'ordre deux.

Si un caractère est à valeurs réelles, comme les valeurs sont des racines de l'unité, elles ne peuvent être égales qu'à 1 ou -1, elle est donc d'ordre deux. Comme il n'existe qu'un élément d'ordre deux, il n'existe qu'un caractère à valeur réelles différent du caractère principal. Or le symbole de Legendre est un caractère non principal. Ce qui termine la démonstration.

Histoire

Les caractères de Dirichlet et leurs séries L furent introduits par Dirichlet, en 1831, en vue de prouver le théorème de Dirichlet à propos de l'infinité des nombres premiers dans les progressions arithmétiques. L'extension aux fonctions holomorphes fut accomplie par Bernhard Riemann.