Carré magique (mathématiques) - Définition

Introduction

un exemple de carré magique.

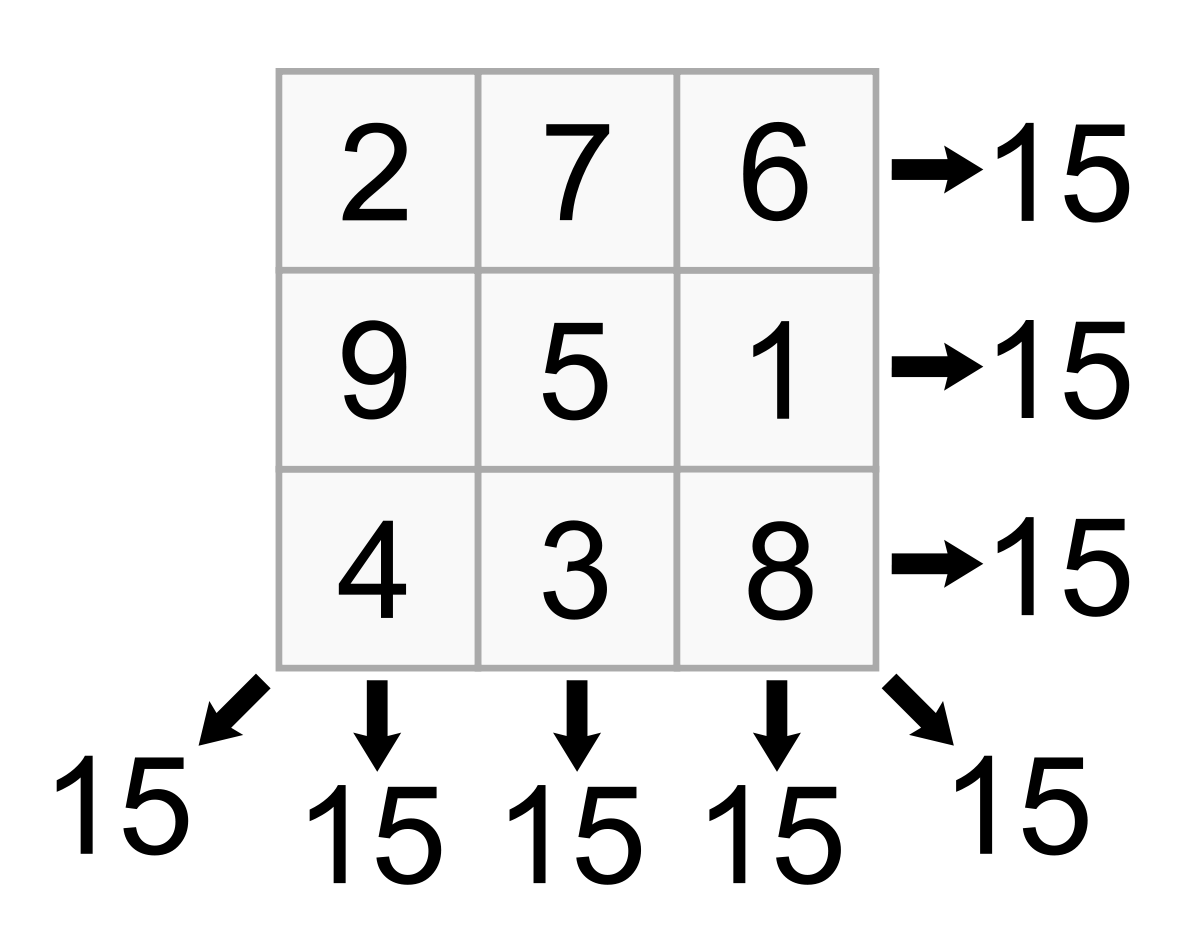
En mathématiques, un carré magique d'ordre n est composé de n² nombres entiers généralement distincts, écrits sous la forme d'un tableau carré. Ces nombres sont disposés de manière à ce que leurs sommes sur chaque rangée, sur chaque colonne et sur chaque diagonale principale soient égales.

Histoire

Les carrés magiques étaient connus des mathématiciens chinois, à partir de -650, et les mathématiciens arabes, probablement vers le VII^e siècle, lorsque les armées arabes firent la conquête du nord-ouest de l'Inde, apprenant des mathématiciens indiens, ce qui incluait certains aspects de la combinatoire. Les premeirs carrés magiques d'ordres 5 et 6 apparurent dans une encyclopédie publiée à Baghdad vers 983, l’Encyclopédie de la Fraternité de la pureté (Rasa'il Ihkwan al-Safa). Des carrés magiques plus simples étaient connus de plusieurs mathématiciens arabes antérieurs. Quelques uns de ces carrés furent utilisés en conjonction avec des « lettres magiques » par des illusionnistes et des magiciens arabes.

Les Arabes seraient les premiers, au X^e siècle, à les utiliser à des fins purement mathématiques. Ahmad al-Buni (en), vers 1250 leur attribue des propriétés magiques.

En Chine (nommés Luoshu : 洛书 selon Le Livre de la rivière Luo), ils furent représentés par différents symboles, puis symbolisés par des chiffres en Inde où furent inventés les chiffres arabes. On les retrouve dans de nombreuses civilisations d'Asie et d'Europe avec généralement une connotation religieuse.

En 1510, le philosophe allemand Cornelius Agrippa (1486-1535), parle de nouveau des carrés magiques, avec toujours une connotation religieuse, il écrit un traité De Occulta Philosophia où il expose une théorie mêlant astrologie et carrés magiques. S'appuyant sur les écrits de Marsilio Ficino et de Pico della Mirandola, il explique les propriétés de sept carrés magiques d'ordre 3 à 9, chacun étant associé à l'une des plannètes astrologiques. Cet ouvrage eut une influence marquée en Europe jusqu'à la Contre-Réforme. Les carrés magiques d'Agrippa continuent à être utilisés lors de cérémonies magiques modernes selon ce qu'il a prescrit.

Simon de La Loubère, diplomate et mathématicien français, publie en 1691 Du Royaume de Siam. Il introduit pour la première fois dans la langue française le terme « carré magique », et expose une nouvelle méthode de construction, dite « méthode siamoise », permettant de construire des carrés d'ordre impair arbitraire.

Au XVII^e siècle, Le juriste et mathématicien français Pierre de Fermat étend le principe des carrés magiques aux cubes magiques. Bernard Frénicle de Bessy écrit un traité sur les carrés magiques (rédigé dans les années 1640, mais publié à titre posthume en 1693) et des tables pour tous les carrés d'ordre 4.

Opérations

La somme de deux carrés magiques du même ordre donne également un carré magique, mais le résultat n'est pas normal, c'est-à-dire que les nombres ne forment pas la suite 1, 2, 3... Également, deux carrés magiques du même ordre peuvent être soustraits.

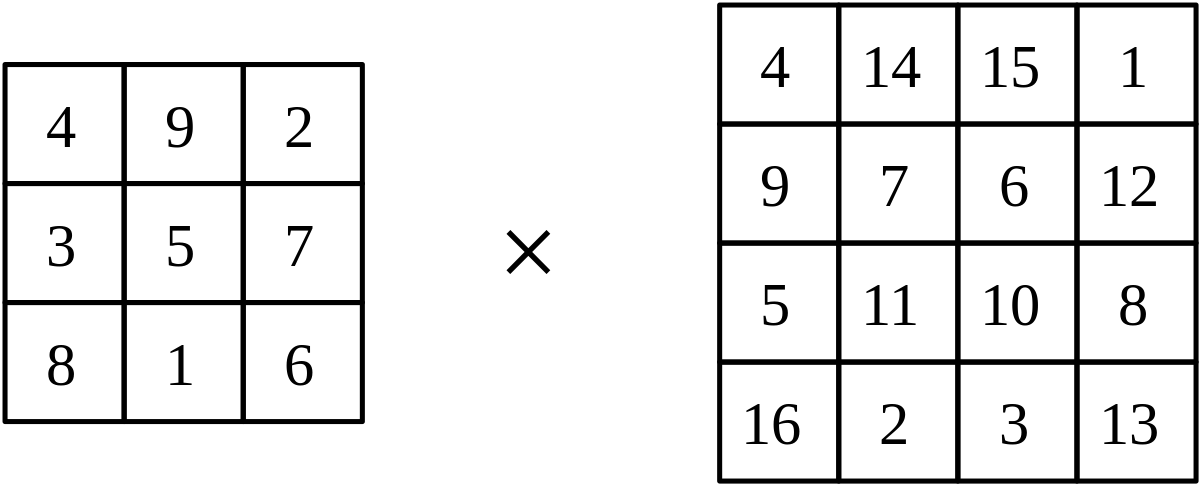
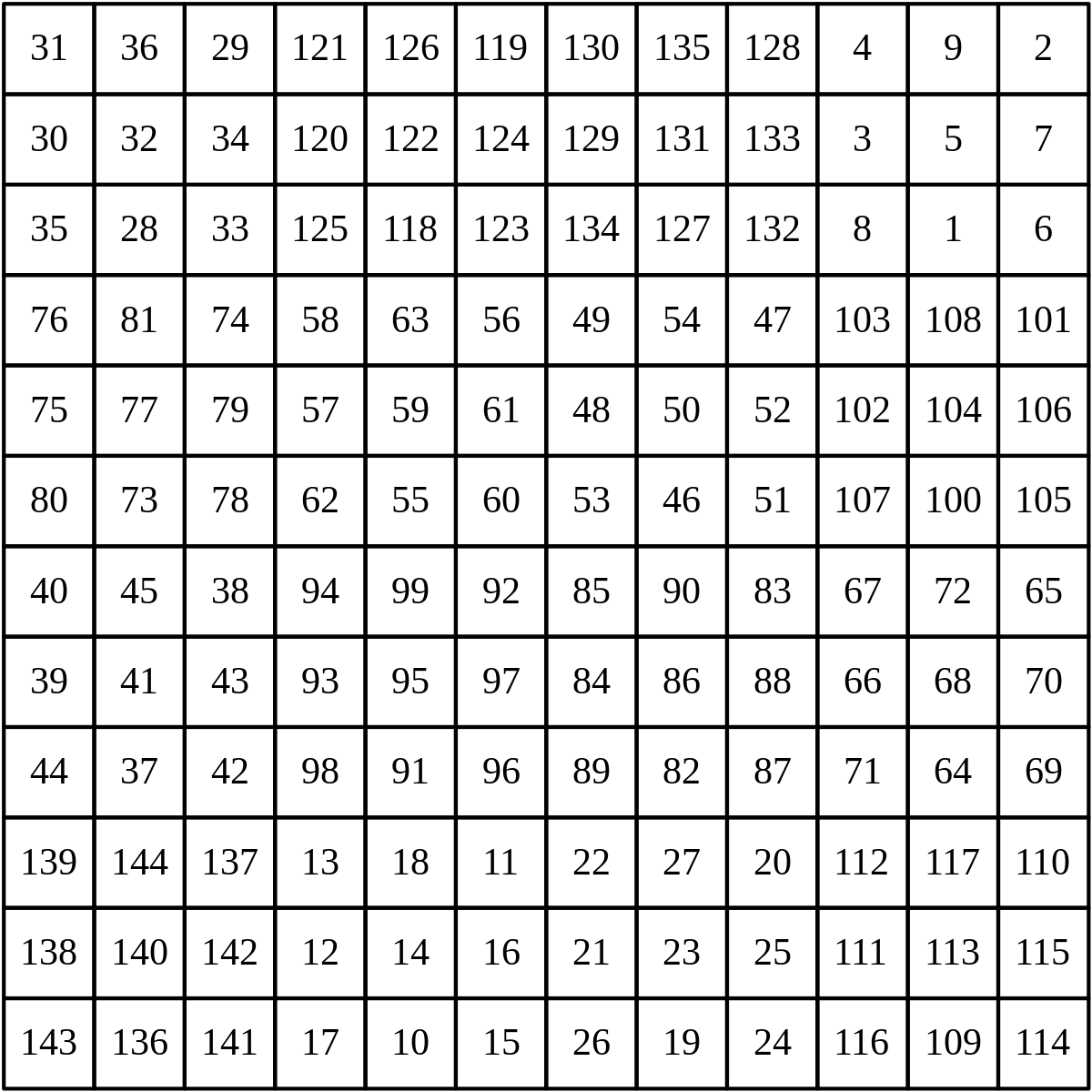
Le « produit » de deux carrés magiques crée un carré magique d'ordre supérieur aux deux multiplicandes. Ce produit s'effectue ainsi. Soit les carrés magiques M et N :

1. Le carré final sera d'ordre MxN.
2. Diviser le damier final en NxN sous-damiers de MxM cases.
3. Dans le carré N, réduire de 1 la valeur de tous les nombres.
4. Multiplier ces valeurs réduites par M × M. Les résultats sont reportés dans les cases de chaque sous-damier correspondant du carré final.
5. Les cases du carré M sont additionnées NxN fois aux cases du damier final.

Soit à effectuer le « produit » de ces deux carrés magiques, un de 3x3 et l'autre de 4x4. Le carré magique final sera de 12x12.

Le carré magique de 3x3 est remplacé par le produit (3 × 3) et chaque nombre dans le carré 4x4 est diminué de 1. Le damier final, de taille 12x12, est divisé en 4x4 sous-damiers, chacun ayant 3x3 cases. Chacune des cases s'obtient en multipliant (3 × 3) par l'une des cases du carré magique 4x4. Par exemple, 117 est le produit de 3 × 3 × 13. Ce carré est magique, mais n'est pas normal. La prochaine étape va « corriger » cette « anomalie ».

Après 4x4 additions du carré 3x3, le carré final est magique et normal.

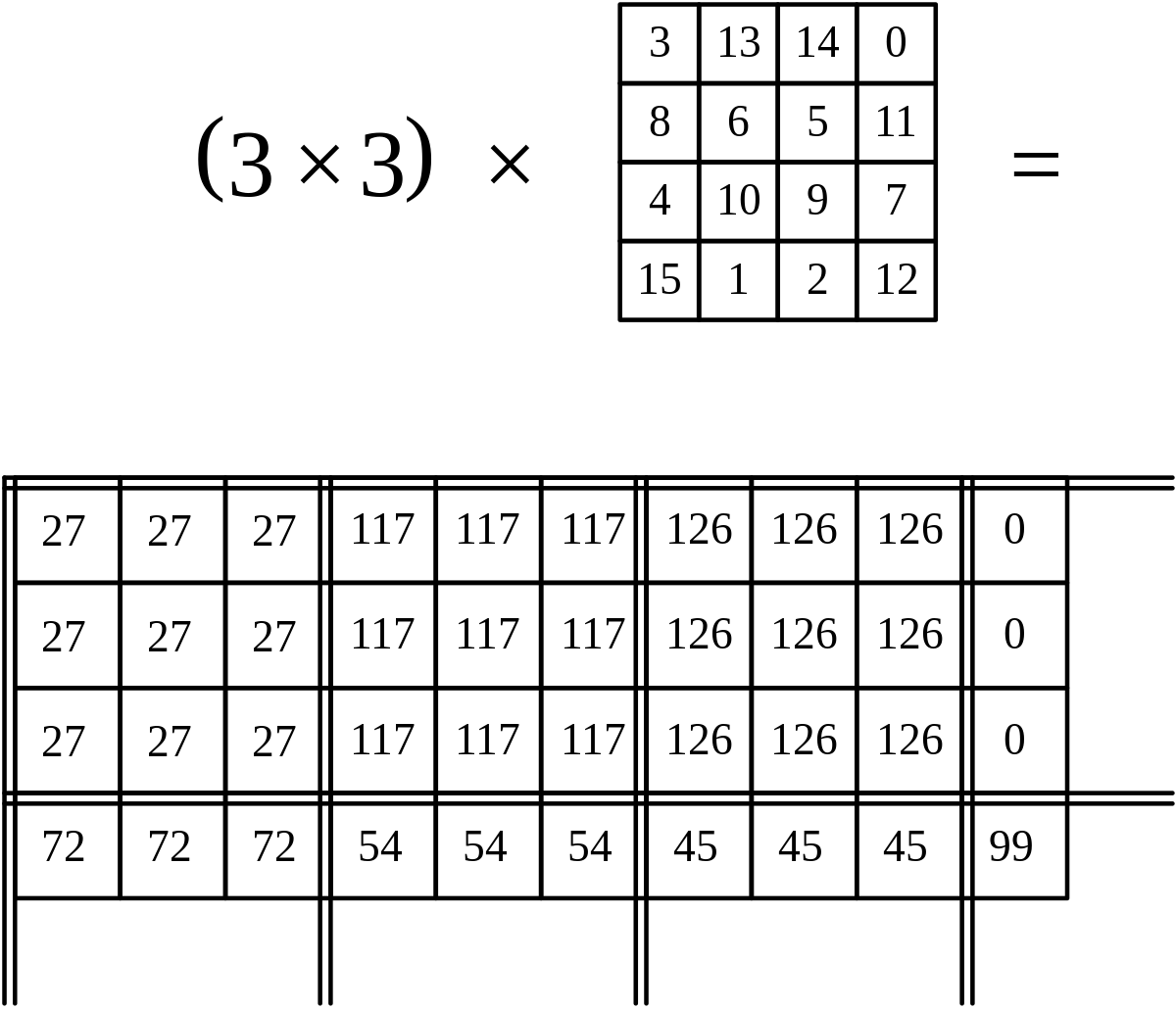
La multiplication de carrés magiques permet de générer des carrés magiques de plus grandes tailles. Cette technique produit plus rapidement des carrés de grande taille que la construction à l'aide de l'une des méthodes directes (celles de la Loubère ou de Strachey, par exemple).