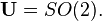Cercle unité - Définition

Cercle unité comme groupe

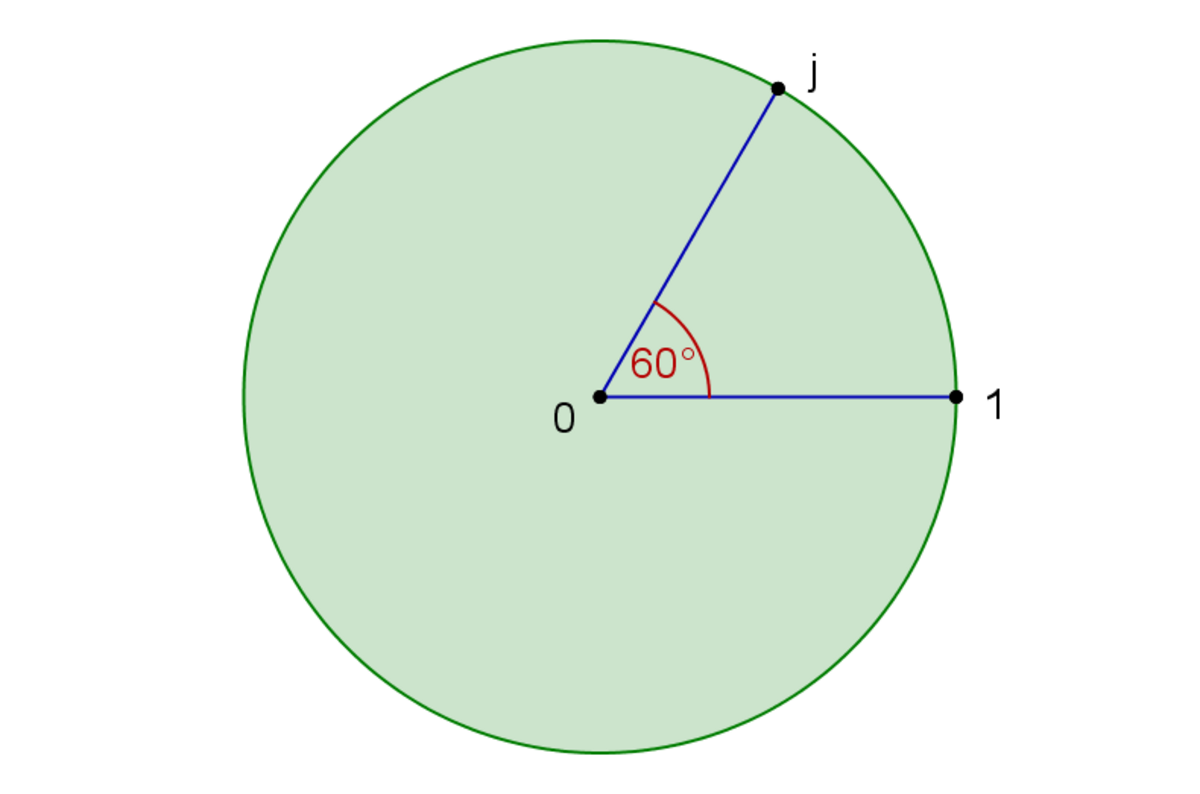
Le cercle unité, en général noté U ou T, est l'ensemble des nombres complexes z dont le module vaut |z|=1. Autrement dit, z appartient à U ssi . Donc, l'inverse de z est son conjugué , lui-même de module 1. De même le produit de deux nombres complexes de module 1 est de module 1. L'ensemble U est donc un groupe pour la multiplication des nombres complexes. Les nombres complexes 1, -1, i et -i appartiennent au cercle unité.

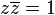
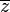
Le cercle unité est le plus grand sous-groupe borné de . Autrement dit, tout sous-groupe borné de est inclus dans le cercle unité U. En particulier, les sous-groupes finis G de sont inclus dans U. Si n est le cardinal de G, alors G est le groupe des racines n-ièmes de l'unité, toutes de module 1. L'application exponentielle, supposée connue, est un morphisme du groupe additif (C,+) vers le groupe multiplicatif (C^*,x). Autrement dit, pour tous w et z,

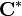
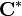
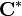
exp(w + z) = exp(w)exp(z).

Si w est un imaginaire pur, alors exp(w) est de module 1. L'image de la droite des imaginaires purs iR est exactement le cercle unité U. En particulier, l'exponentielle définit un morphisme surjectif de groupes . Ce morphisme est périodique, et la période est 2π. Dans l'enseignement supérieur, cette propriété peut être présentée comme la définition du nombre Pi. Cette définition remonte au début du XX^e siècle. Le noyau de ce morphisme est donc le sous-groupe additif 2iπZ de iR.

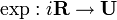
De plus, tout nombre complexe non nul z s'écrit z = | z | w où w = exp(iθ) est de module 1. Le nombre réel θ bien défini modulo 2π est appelé l'argument de z.

Groupe des rotations

Rotation de 60 degrés, envoyant 1 sur j.

Les nombres complexes non nuls représentent les similitudes directes du plan euclidien orienté. Plus exactement, le module sur C est une norme euclidienne dont le produit scalaire associé est

ou, si on préfère, < a + ib | a' + ib' > = aa' + bb'.

La multiplication à gauche par z = re^iθ est la similitude directe d'angle θ et de rapport r. En particulier, si le nombre complexe w est de module 1, alors la multiplication par w est la rotation d'angle θ. On note en général SO(2) le groupe des rotations d'un plan euclidien. La description précédente donne

Groupe de Lie

La lecture de cette partie nécessite de connaitre les bases de la géométrie différentielle et notamment la définition d'une variété différentielle.

L'application est différentiable en dehors de 0, et 1 en est une valeur régulière. Le cercle unité U, par définition image réciproque de 1, est une sous-variété différentielle de C. Le cercle unité U est alors un sous-groupe de Lie de C^*.

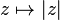
Remarque : le groupe multiplicatif C^* est un groupe de Lie complexe. Tout groupe de Lie complexe admet un sous-groupe de Lie réel compact maximal, qui est appelé sa forme réelle. La forme réelle de C^* est le cercle unité U. Ce sont là des propriétés remarquables, mais qui n'ont pas d'incidence dans l'étude de U.

Tout groupe de Lie connexe compact de dimension est isomorphe à T.

Ici, la notation T est préférable. Plus généralement, tout groupe de Lie compact connexe et commutatif est isomorphe à un "tore", c'est-à-dire au quotient de R_k par Z_k, en général noté T^k. Ce tore T^k est isomorphe au produit direct de k copies de T.