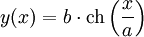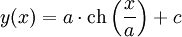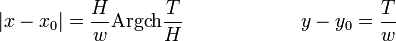Chaînette - Définition

Définition mathématique

L’équation cartésienne de la forme de la chaînette est :

,

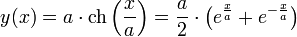
dans laquelle ch désigne le cosinus hyperbolique.

est le rapport de la composante horizontale H de la tension T au poids linéique w, poids par unité de longueur.

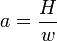
Cette équation dépend d’un seul paramètre a (une constante, qui a la dimension d’une longueur dans son interprétation physique). Une courbe d’équation :

n’est généralement pas une chaînette au sens strict. Cependant, la forme de la courbe ne varie pas à une constante additive près (déterminant sa hauteur de portée), et la courbe suivante sera considérée aussi comme une chaînette généralisée :

On peut également la voir sous la forme d’une équation paramétrique :

Il peut être commode de prendre pour paramètre la tension qui croît avec l'altitude du point. Dans ces conditions, par rapport à des axes quelconques :

Si l'allongement de la ligne ne peut être négligé, la longueur au repos dl d'un petit élément devient sous tension, conformément à la loi de Hooke :

(E : module d'Young, A : section de la ligne)

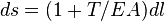
Les projections horizontale et verticale du petit élément étant modifiées dans les mêmes proportions, pour obtenir les équations paramétriques correspondantes, il faut différentier les deux équations précédentes, multiplier les résultats par le facteur d'accroissement et intégrer de nouveau. Chacune des deux équations contient alors un second membre corrigé par un terme inversement proportionnel à la rigidité EA et la courbe résultante n'est plus une chaînette.

Propriétés et applications

• L'axe des ordonnées est axe de symétrie de la courbe. Pour l'axe des abscisses, on parle de base.
• La chaînette est un cas particulier d'alysoïde et de courbe de Ribaucour.
• La chaînette est presque verticale près des points de suspension, car c'est là que le poids le plus important tire le plus la chaîne vers le bas. En revanche, vers le bas de la courbe, l'inclinaison diminue peu à peu puisque la chaîne supporte de moins en moins de poids. C'est d'ailleurs une des différences entre la chaînette et la parabole : pour une longueur égale, la parabole est plus « pointue » dans sa partie inférieure.
• La chaînette n'apparaît pas seulement dans la forme d'un fil suspendu. On la trouve aussi :
  • renversée, pour un arc tenant par son propre poids. Relèvent de cette technique les essais architecturaux de Gaudi, l'arche du Jefferson National Expansion Memorial à Saint Louis, et le hangar à dirigeables d'Écausseville. La voûte nubienne est aussi basée sur une forme de chaînette renversée.
  • verticale, dans le profil d’une voile rectangulaire attachée à 2 barres horizontales, enflée par un vent soufflant perpendiculairement à ces barres, en négligeant le poids propre de la voile par rapport à la force du vent. C'est cette propriété qui justifie le nom de « vélaire » (voile) donné par Jacques Bernoulli.

Aspects pratiques

• La solution du problème est simple si l'on se donne les caractéristiques de la ligne (longueur et poids linéaire) et la force appliquée à une extrémité pour calculer son extension (distances horizontale et verticale) et la force à l'autre extrémité. Les formules correspondantes définissent le module de base de tout calcul.
• Si l'élasticité de la ligne ne peut plus être négligée, elle est prise en compte en appliquant la loi de Hooke, ce qui entraîne simplement une complication du calcul de l'extension dans le module de base.
• Si les lignes sont constituées par une succession de segments de caractéristiques différentes, l'appel répété du module de base permet d'obtenir pour la ligne un résultat analogue à celui du segment en transmettant les forces d'un segment à un autre et en totalisant les extensions.
• S'il existe un fond sur lequel repose une partie de la ligne, la force verticale appliquée à une extrémité permet de déterminer la longueur suspendue non déformée à ajouter à la longueur posée sur le fond.
• Dans tous ces cas, il est donc possible d'obtenir pour la ligne un module qui transforme les caractéristiques de la ligne et la force à une extrémité en l'extension et la force à l'autre extrémité. Malheureusement, ces calculs relativement simples ne sont pas adaptés aux problèmes concrets dans lesquels on souhaite généralement calculer les forces aux deux extrémités en fonction des caractéristiques et de l'extension. Deux boucles de dichotomie, inconditionnellement convergentes, résolvent le problème.