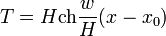Chaînette - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la chaînette est une courbe plane transcendante, qui correspond à la forme que prend un câble (ou une chaîne) lorsqu'il est suspendu par ses extrémités et soumis à une force gravitationnelle uniforme (son propre poids). On lui donne parfois le nom de vélaire.
Étymologie et histoire
Le problème de la forme prise par un fil pesant flexible a intéressé très tôt les mathématiciens. Galilée pensait que cette forme devait être un arc de parabole, mais la preuve du contraire fut apportée en 1669 par Jungius, après une première remise en cause par Huygens en 1646.
En 1691, Leibniz, Jean Bernoulli et Huygens, sous l’impulsion d’un défi lancé par Jacques Bernoulli, démontrent quasi simultanément que la forme exacte est une chaînette. C’est d’ailleurs Huygens qui la baptise ainsi, dans une lettre adressée à Leibniz. Délaissant le vocable latin du problema funicularium, (problème relatif à la corde), utilisé par les Bernoulli, il utilise le mot catenaria, courbe relative à la chaîne (catena), puis passe au français chaînette, renouant ainsi avec le terme catenella utilisé par Galilée (alors que les mathématiciens anglophones conserveront la désignation de Huygens pour la nommer catenary, le même mot anglais étant traduit en français par caténaire avec la même origine latine, mot utilisé aussi en français pour certaines constructions autoportées en forme de chaînette).
Certains auteurs francophones lui donnent donc aussi le nom de caténaire bien que la caténaire désigne plutôt l’association d’un câble autoporté (en forme de chaînette) soutenant un second câble linaire dans sa partie inférieure, les deux câbles étant soumis à une force de traction longitudinale équilibrée par une série de pendules, le système de portage déformant la chaînette porteuse pour lui donner une forme plus proche en fait de la parabole, la chaînette n'étant présente virtuellement que dans l'axe central entre les deux câbles où sont articulés les pendules de longueur variable.
Calcul mécanique
La théorie de la chaînette décrit la courbe d'équilibre d'une ligne (chaîne ou câble) suspendue entre deux points, homogène, inextensible, sans rigidité en flexion, soumise à son seul poids. Cette dernière condition assure que toute la courbe est située dans un plan vertical, le système de coordonnées étant naturellement x horizontal, y vertical.
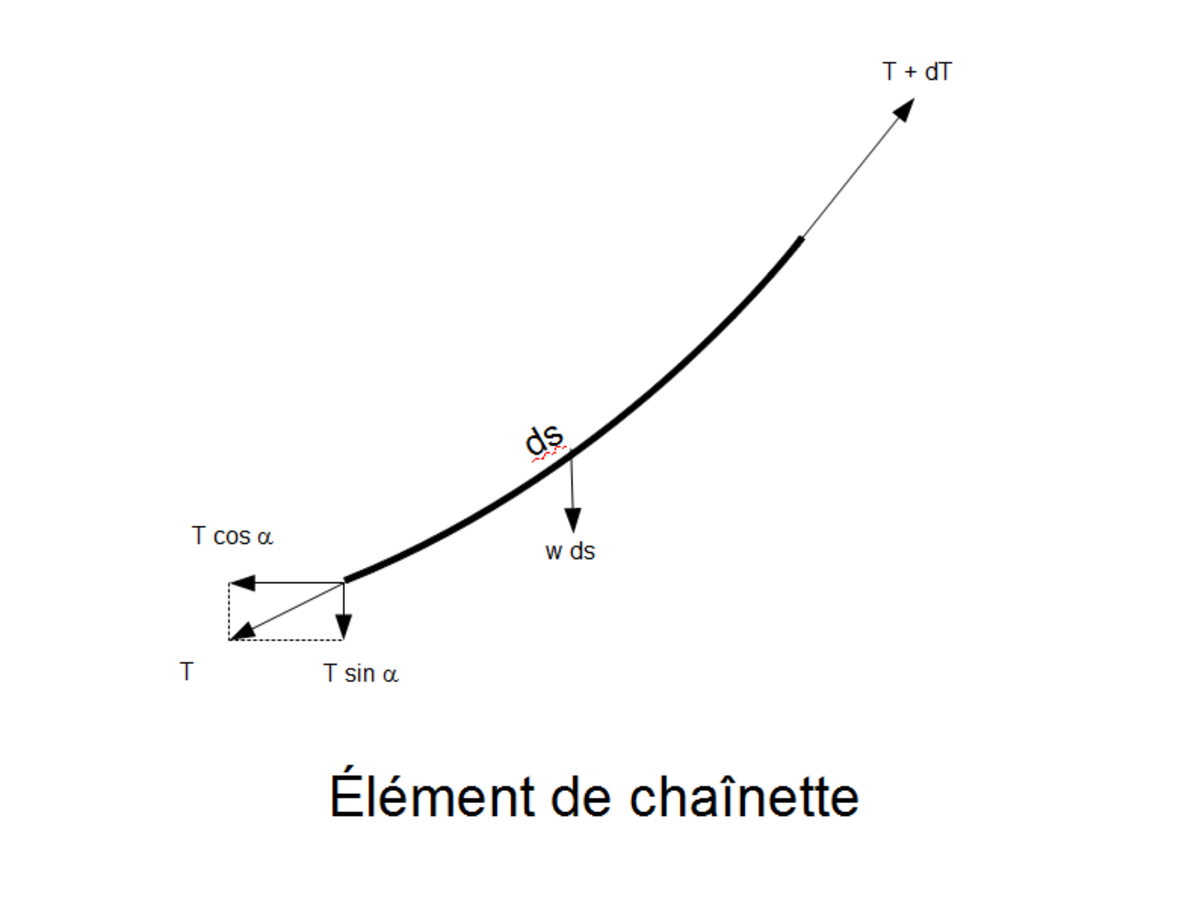
Pour établir les conditions d'équilibre on raisonne comme en résistance des matériaux en coupant par la pensée la ligne en un point arbitraire et en faisant apparaître les forces de liaison. En l'absence de rigidité en flexion il n'y a ni effort tranchant ni moment fléchissant mais un seul effort axial T nommé tension, α étant l'angle de celle-ci avec l'horizontale. Ainsi la composante horizontale s'écrit Tcosα et la composante verticale Tsinα.
L'absence de rigidité en flexion crée par contre des grandes déformations qui conduisent à étudier l'équilibre d'un petit élément de longueur ds . Il subit une force horizontale nulle et une force verticale égale à son poids wds (où w est le poids par unité de longueur), ce qui conduit aux équations différentielles
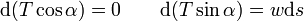
L'intégration de la première équation donne
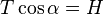
La seconde donne
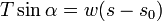
En élevant au carré et en sommant on obtient la loi de variation de la tension en fonction de l'abscisse curviligne :
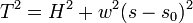
En divisant les deux équations de base on obtient la pente de la courbe :
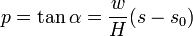
La dérivation par rapport à x conduit à
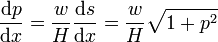
L'intégration donne
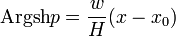
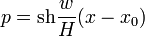
Une nouvelle intégration donne l'équation de la chaînette :
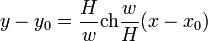
De la pente on déduit également l'abscisse curviligne :
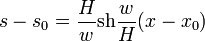
ainsi que la composante verticale de la tension :
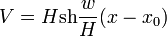
D'où la tension elle-même :