Choc élastique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

Un choc élastique est un choc entre deux corps qui produit un rebond entièrement régi par l'élasticité des zones d'impact. Ça signifie que les corps reprennent leur forme initiale, sans déformation permanente comme dans un écrasement (crash).
Il se modélise en mécanique du solide par une collision élastique, c'est-à-dire sans dissipation. Le système composé des corps qui se heurtent conserve :
- son énergie cinétique, du fait de l'absence de dissipation,
- sa quantité de mouvement, comme tout système isolé.
La vitesse relative entre les objets est la même (de sens opposé) avant et après la collision. Autrement dit, le coefficient de restitution (rapport des vitesses relatives) est égal à 1. On parle parfois aussi de choc dur (par opposition à un choc mou).
La collision élastique s'oppose à la collision inélastique pour laquelle l'énergie cinétique n'est pas conservée (les corps qui se heurtent peuvent, par exemple, absorber de l'énergie par déformation plastique).

Formulation pour deux corps
Si on considère le choc de deux corps 1 et 2 et :
-
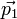
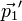
-
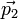
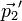
-
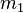
-
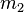
-
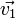
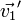
-
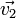
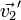
Le théorème de conservation de la quantité de mouvement donne :
La conservation de l’énergie cinétique totale donne :
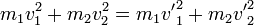
Étant donné que
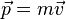
Choc élastique en relativité restreinte
Le problème du choc élastique en mécanique relativiste est traité dans l'article sur la relativité restreinte.
Exemples de résolution
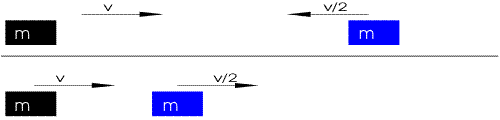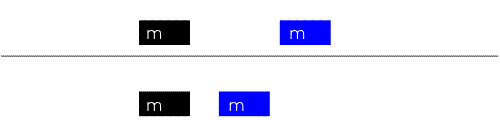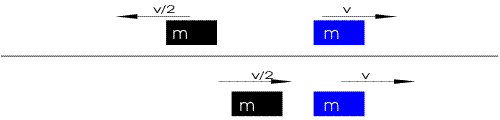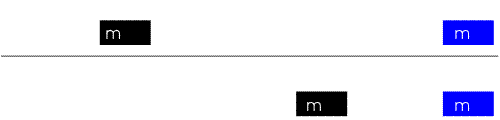
Choc direct de deux points
Si une collision est dite directe, les vecteurs vitesse des points avant et après collision sont portés sur un même axe. En projetant dessus, le système (1) peut donc se simplifier sous la forme :
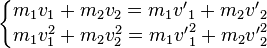
La résolution de ce système donne les vitesses après choc en fonction des masses et vitesses initiales :
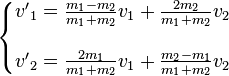
Résolution sous forme vectorielle dans le cas de masses ponctuelles
Si
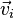
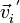
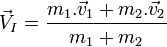
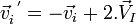
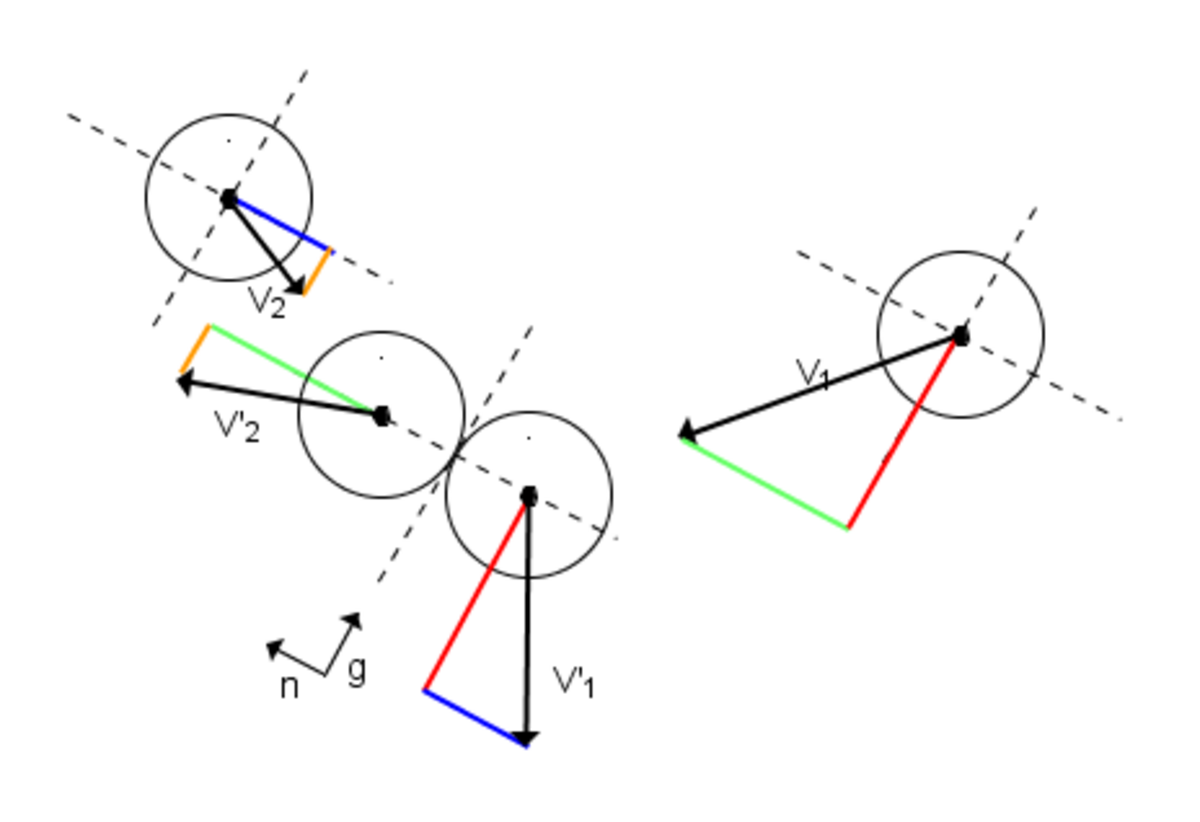
Choc de 2 boules de même masse
Lorsque les 2 boules ont la même masse, elles échangent simplement leurs quantités de mouvement normales par rapport au « plan de collision » (bleu et vert) et conservent leurs vitesses tangentielles (orange et rouge).
Le point de contact est facilement déterminé en résolvant l'équation du second degré d'inconnue t suivante:
![[(\vec{op_1} + \vec{v_1}t) - (\vec{op_2} + \vec{v_2}t)]^2 = 4r^2](https://static.techno-science.net/illustration/Definitions/autres/f/f160ab59a841a2146ae1654355b9ffbb_02143d4882d345d91a085b8aae9c7d7f.png)
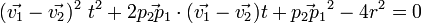
ou pn est la position de la boule n,
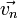
// Calcul de la collision entre 2 boules // de même masse et de rayon r en 2D (ex: boules de billard) // Les boules sont positionnées au point de contact // (m.x,m.y) = centre de la boule m (repère de l'image) // (m.vx,m.vy) = vitesse de la boule m avant le choc (repère de l'image) // Calcul de la base orthonormée (n,g) // n est perpendiculaire au plan de collision, g est tangent double nx = (m2.x - m1.x)/(2*r); double ny = (m2.y - m1.y)/(2*r); double gx = -ny; double gy = nx; // Calcul des vitesses dans cette base double v1n = nx*m1.vx + ny*m1.vy; double v1g = gx*m1.vx + gy*m1.vy; double v2n = nx*m2.vx + ny*m2.vy; double v2g = gx*m2.vx + gy*m2.vy; // Permute les coordonnées n et conserve la vitesse tangentielle // Exécute la transformation inverse (base orthonormée => matrice transposée) m1.vx = nx*v2n + gx*v1g; m1.vy = ny*v2n + gy*v1g; m2.vx = nx*v1n + gx*v2g; m2.vy = ny*v1n + gy*v2g;