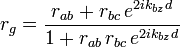Coefficients de Fresnel - Définition

Introduction

Amplitudes de réflexion et de transmission d'une onde franchissant un dioptre vers un milieu d'indice de réfraction supérieur.

Les coefficients de Fresnel, introduits par Augustin Jean Fresnel (1788-1827), interviennent dans la description du phénomène de réflexion-réfraction des ondes électromagnétiques à l'interface entre deux milieux, dont l'indice de réfraction est différent. Ils expriment les liens entre les amplitudes des ondes réfléchies et transmises par rapport à l'amplitude de l'onde incidente.

Généralités

Schéma le la réflexion-transmission d'une onde plane à lors d'un saut d'indice

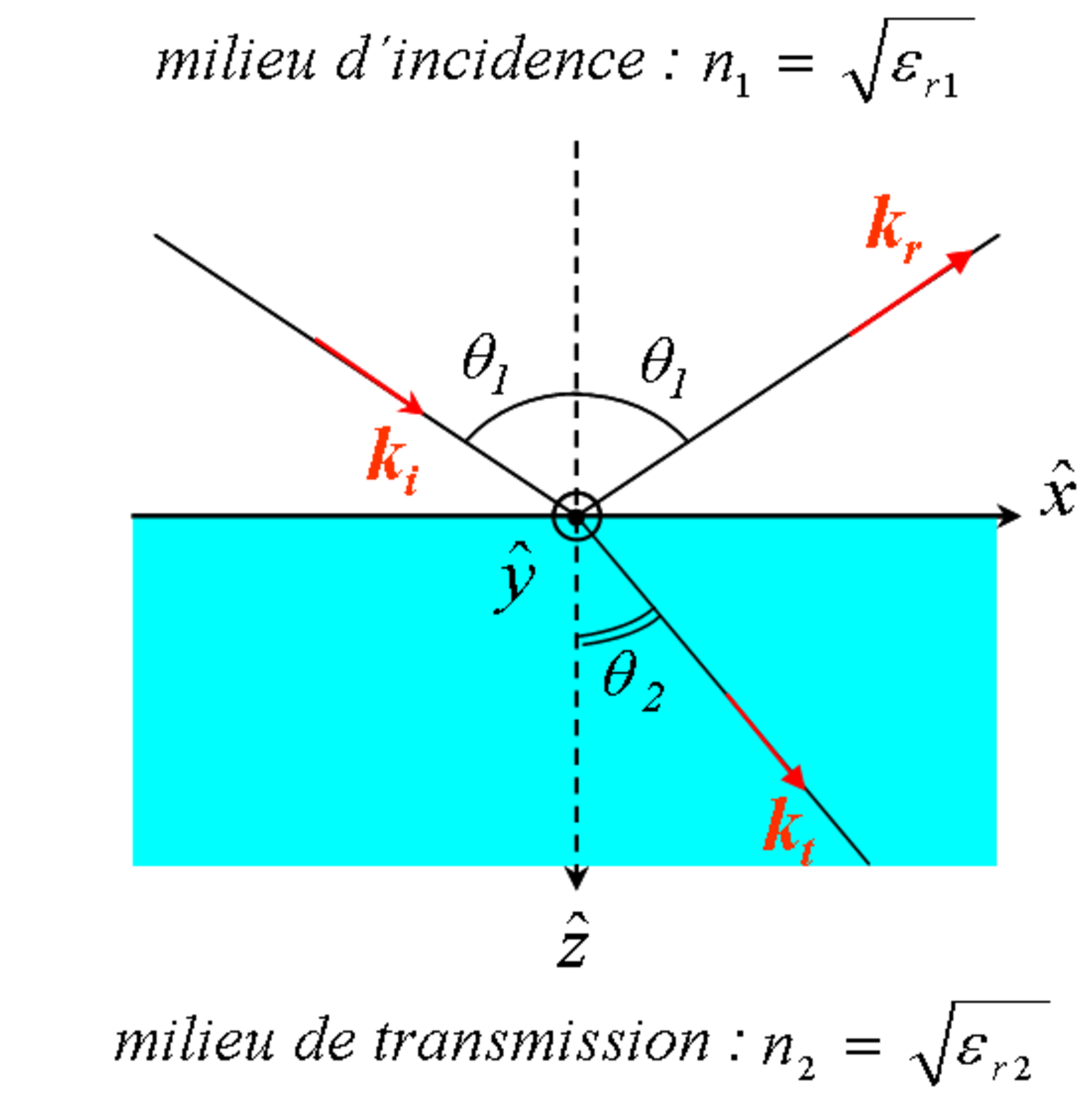
On définit le coefficient de réflexion en amplitude r et le coefficient de transmission en amplitude t du champ électrique par :

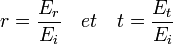
où E_i, E_r et E_t sont les amplitudes associées respectivement au champ électrique incident, réfléchi et transmis (réfracté).

En général, ces coefficients dépendent:

• des constantes diélectriques des milieux d'entrée et de sortie, respectivement ε₁ et ε₂
• de la fréquence f de l'onde incidence
• des angles d'incidence θ_i=θ₁ et de réfraction-transmission θ_t=θ₂,
• de la polarisation des ondes. Polarisation de l'onde qui peut éventuellement être modifiée pendant le franchissement de l'interface.

Ils sont obtenus en considérant les relations de continuité à l'interface des composantes tangentielles des champs électriques et magnétiques associés à l'onde.

Extension au cas des interfaces multiples

On peut définir des coefficients de Fresnel globaux pour un système constitué de plusieurs couches de milieux d'indices différents.

On considère pour les calculs suivants les permittivittés diélectriques et non les indices de réfraction afin d'alléger les notations.

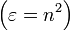
Cas de deux interfaces

Réflexions multiples entre deux interfaces

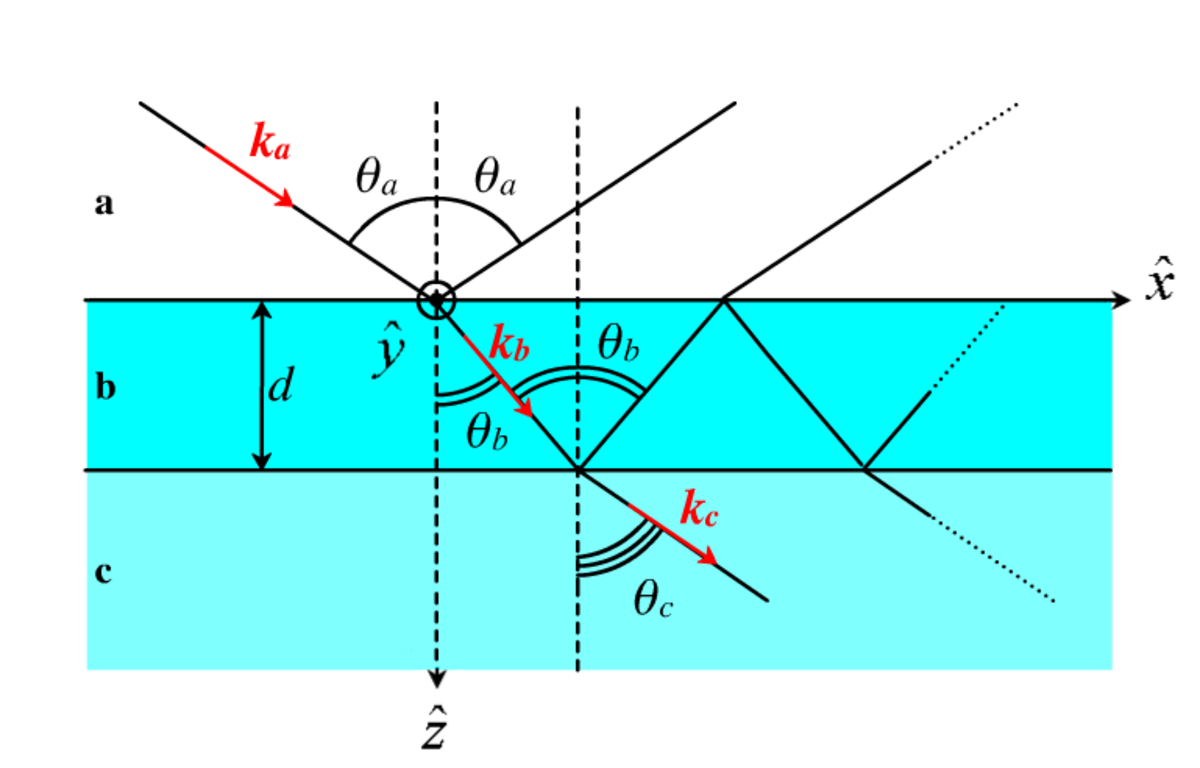
Considérons 3 milieux M_a, M_b et M_c de permittivités diélectriques consécutives différentes, séparés par 2 interfaces planes.

Notations:

• Soit d l'épaisseur de M_b (M_a et M_b sont semi-infinis).
• Soient θ_i et θ_j respectivement les angles d'incidence et de refraction à l'interface entre M_i et M_j (avec i,j = a,b ou b,c)
• Soit la composante suivant z du vecteur d'onde dans M_b
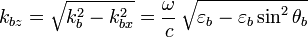
• Soit r_ij le coefficient de réflexion entre M_i et M_j tel que défini précédemment (r_ij dépend de la polarisation TM ou TE, ainsi que des angles θ_i et θ_j, avec i,j = a,b ou b,c)

Formule:

Le coefficient de réflexion global s'écrit alors :

Cette relation décrit aussi bien le comportement de la simple lame à face parallèle que les cas plus spectaculaires des couches antireflet ou la génération des plasmons de surface : on joue pour ce faire sur les constantes diélectriques et l'épaisseur du milieu intermédiaire en fonction des indices des milieux extrêmes.

Cas de n interfaces

En partant des résultats précédents on peut définir par récurrence les coefficients de Fresnel globaux pour n interfaces.

Considérons n+1 milieux, de permittivités diélectriques consécutives différentes, séparés par n interfaces planes.

Notations:

• Soit M_p le p-ième milieu. 1 ≤ p ≤ n+1
• Soit d_p l'épaisseur de M_p (2 ≤ p ≤ n car M₁ et M_n+1 sont semi-infinis)
• Soient θ_p et θ_p+1 respectivement les angles d'incidence et de refraction à l'interface entre M_p et M_p+1
• Soit la composante suivant z du vecteur d'onde dans le p-ième milieu
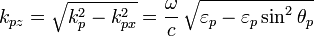
• Soit r_p,p+1 le coefficient de réflexion entre M_p et M_p+1 tel que défini précédemment (r_p,p+1 dépend de la polarisation TM ou TE, ainsi que des angles θ_p et θ_p+1)

Algorithme:

On part de U_n = r_n,n+1, puis pour p = n jusqu'à 2 on utilise la relation de récurrence :

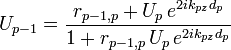
Le coefficient de réflexion global s'écrit alors r_g = U₁