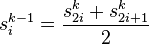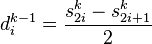Compression par ondelettes - Définition

Introduction

La Compression par ondelettes est une technique de compression de données, bien adaptée à la compression d'images.

Introduction aux ondelettes

Grande rivale de la DCT, la technique de compression à base d’ondelettes offre une plus grande finesse au niveau de l’analyse du signal et permet de mieux s’adapter aux propriétés locales de l’image. Il s’agit d’une voie de recherche assez prometteuse. Les codeurs JPEG 2000 et SPIHT utilisent tous deux une transformée en ondelettes dans leur schéma de compression. En revanche, seule JPEG 2000 est une norme. La compression en ondelettes est en elle-même sans pertes. C'est l'introduction d'une quantification ou d'un seuillage qui entraine la perte irréversible d'informations.

La transformation par ondelettes est une technique inventée par Jean Morlet, un ingénieur français, pour la prospection pétrolière. Cette technique consiste à décomposer une image en une myriade de sous-bandes, c’est-à-dire des images de résolution inférieure.

La transformation en ondelettes provient d'une analyse multirésolution de l'image. On considère des espaces d'approximations de plus en plus grossiers notés V_j et des espaces "capturant" les détails perdus entre chaque niveau d'approximation notés W_j avec . Les bases ondelettes se situent sur les W_j, c'est là qu'est le cœur de la compression sans perte.

Les coefficients d'ondelettes dans les W_j mettent en évidence des informations sur les contours, les textures, leur localisation et leur orientation. Le choix de l’ondelette mère est très important et fait toujours l’objet d’expérimentations pour adapter l’analyse du signal image au système de perception visuelle de l’homme.

Transformée ondelettes

Pour commencer, nous allons expliquer la transformée à une dimension.

Nous avons donc comme donnée originale :

Niveau 4 :

Étape après étape, nous obtenons :

Niveau 3 :

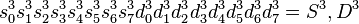
Niveau 2 :

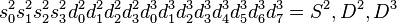
Niveau 1 :

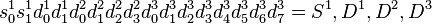
Nous obtenons finalement :

Niveau 0 :

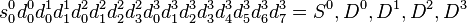
Le passage d’un niveau à l’autre s’effectue, avec une ondelette de Haar, à l’aide des formules suivantes :

Équation 1 : Transformée ondelettes

Le premier calcul est la moyenne de deux pixels ce qui va permettre de calculer les fréquences deux fois plus basses. Le deuxième calcul est la différence entre deux pixels, ce qui correspond à l’amplitude de la fréquence à l’endroit donné. On remarque donc que la transformée DCT donne des informations sur l’amplitude des fréquences, alors que la transformée en ondelettes donne l’amplitude de la fréquence à un endroit donné. Cette dernière donne donc un rendu plus proche de la perception humaine car pour le son par exemple, on remarque s’il y a des basses ou des aigus à un instant donné. On peut également remarquer que dans le cas de la DCT, les fréquences varient de façon linéaire tandis que dans le cas de la transformée par ondelettes les fréquences varient de manière logarithmique. Ceci est également plus proche de notre perception.

Algorithme ondelettes

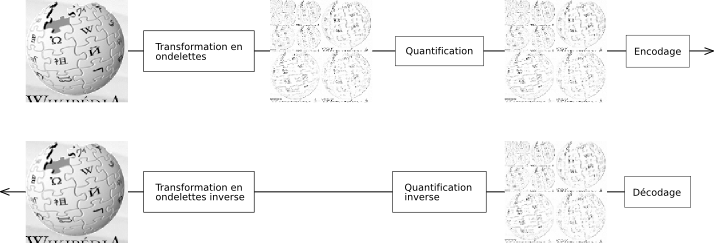
Figure 1 : schéma de compression

La compression se compose donc des étapes suivantes :

1. Transformations par ondelettes.
2. Quantification : les valeurs des images de détails inférieures à un certain niveau sont éliminées, en fonction de l’efficacité recherchée. C’est cette étape qui introduit des pertes.
3. Codage des valeurs restantes.