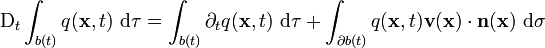Concepts de base en théorie des milieux continus - Définition
La liste des auteurs de cet article est disponible ici.
Mouvements incompressifs et milieux incompressibles
Comme corollaire de la relation d'Euler, il est clair que pour un matériau incompressible, le champ de vitesse associé à un mouvement quelconque possible doit être indivergentiel (on dit aussi solénoïdal), c'est-à-dire
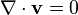
En effet, pour un matériau incompressible, le coefficient d'incompressibilité (= module de compression) κ est infiniment grand. Cela implique que pour n'importe quelle transformation J(t) = 0. Toutefois, il faut insister sur le fait que la conclusion réciproque n'est pas vraie : on ne peut pas conclure du fait qu'un mouvement est indivergentiel que le milieu qui se déforme est lui-même incompressible. Beaucoup d'exemples de mouvements indivergentiels se passant dans des milieux compressibles, ou hautement compressibles tels que l'atmosphère terrestre, se rencontrent dans la nature. Il convient donc de soigneusement faire la distinction entre un mouvement incompressif (∇ · v = 0) et un milieu incompressible (κ = ∞). Malheureusement, beaucoup d'auteurs ne font pas cette distinction sémantique, et causent ainsi parfois de sévères confusions. Dans le même ordre d'idées, il faut prendre soin de distinguer entre les concepts de piézotropie (se rapportant à une déformation) et de barotropie (se rapportant à un milieu), qui sont aussi confondus par certains auteurs.
Dilatation cubique et relation d'Euler
Enfin, nous allons terminer ce survol des concepts fondamentaux de la théorie des milieux continus en introduisant le concept de dilatation cubique Θ. Celle-ci est définie comme le rapport de l'élément de volume δυ attaché à un point massique ξ déterminé à un instant quelconque t à l'élément de volume δυo attaché au même point massique ξ à l'instant initial t = 0. En d'autres termes, la dilatation cubique correspond au déterminant jacobien de la transformation ponctuelle par laquelle le volume à l'instant initial devient le volume à un instant quelconque, soit
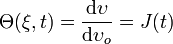
On montre aisément que la dérivée matérielle relative de la dilation cubique représente la divergence du champ de vitesse, c'est-à-dire
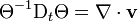
Cette relation est due à Leonhard Euler. On en tire l'importante conclusion que la signification physique de la divergence d'un champ de vitesse correspond au taux de changement relatif du volume d'un point massique le long de la trajectoire du mouvement.
Bibliographie
- R. Aris (1962). Vectors, Tensors, and the Basic Equations of Fluid Mechanics, Prentice-Hall, Englewood Cliffs, N.J. [Une édition légèrement corrigée est parue en 1989 chez Dover Publications, New York]. ISBN 0-486-66110-5.
- L. Sedov (1971). A course in continuum mechanics, volume 1. Basic equations and analytical techniques, Wolters-Noordhoff Publishing, Groningen. ISBN 90-01-79680-X.
Théorème de transport de Reynolds
La formule cinématique d'Euler, DtJ = J ∇ ⋅ v, établie ci-dessus, a comme conséquence un théorème de cinématique important, connu sous l'appellation de « théorème de transport de Reynolds », qui exprime le taux de changement dans le temps d'une quantité physique q dans un volume arbitraire de matière. Ce théorème peut se formuler mathématiquement ainsi : Soit b(t) une portion quelconque se déformant au cours du temps d'un volume matériel B(t). On suppose que sa frontière ∂b(t) est régulière, et que la normale unitaire n(t) en un point quelconque de ∂b(t) est orientée vers l'extérieur. Pour une quantité physique arbitraire q associée à un point matériel appartenant au volume b(t) ou à sa frontière ∂b(t), on a alors
ou encore, en utilisant le théorème de la divergence de Gauss,