Concepts de base en théorie des milieux continus - Définition

Introduction

Cet article traite des concepts de base en théorie des milieux continus.

De nombreux articles de Wikipédia traitent de milieux continus dans le cadre de différents domaines de la physique : mécanique, hydrodynamique, élasticité, rhéologie, électromagnétisme, etc. Le but de cet article est de dégager les concepts de base communs à tous ces domaines, en le plaçant dans le cadre de la géodynamique, science qui fait appel à tous ces domaines à la fois.

Notion de continuum et description lagrangienne

Dans les problèmes de dynamique de la Terre, celle-ci est généralement traitée comme un système de volumes adjacents remplis continûment de matière séparés par des surfaces-frontière. Une telle approche phénoménologique ne considère pas la structure atomique et moléculaire de la matière, et suppose que chaque point massique est constitué par un nombre suffisant d'atomes ou molécules pour donner un sens au fait d'associer à ce point des propriétés macroscopiques, par exemple une température, une pression, une position, une vitesse, etc., qui représentent des moyennes au sens de la physique statistique. Dans un sens mathématique, un point massique (on parle encore de « particule ») doit être suffisamment petit pour coïncider, à chaque instant, avec un point donné de l'espace. Un tel point de l'espace est une entité purement géométrique, sans extension dans l'espace et dépourvu d'attributs physiques par lui-même : ainsi, si nous considérons une propriété d'un milieu continu (ou «continuum» en jargon technique) en un quelconque point de l'espace, nous nous reférons à la propriété attachée au point massique qui coïncide avec ce point de l'espace juste à l'instant considéré.

Un continuum est un ensemble dénombrable de points massiques dans l'espace, de telle manière que lorsqu'on considère un voisinage arbitrairement petit d'un élément quelconque de cet ensemble, il existe dans ce voisinage encore au moins un autre point massique appartenant au même continuum. Le mouvement d'un continuum déformable est entièrement spécifié seulement en termes des mouvements respectifs de tous ses points massiques ; en général, les mouvements d'un sous-ensemble de points massiques ne décrivent pas complètement le mouvement d'ensemble d'un milieu continu déformable.

Par conséquent, il est nécessaire d'individualiser les points d'un continuum en trouvant une quelconque façon de les répertorier, de les nommer. Ce but est atteint au moyen de la description lagrangienne, dans laquelle les différents points massiques sont répertoriés grâce à leur position ξ = ξⁱg_i (ou des fonctions connues de celle-ci) à un instant t = t_o pris comme référence ; le plus souvent, il s'agit de l'instant initial t = 0. Les g_i sont des vecteurs de base covariants, définis ici dans l'espace physique E₃, appartenant à la métrique de l'état initial non déformé, et les composantes contravariantes ξⁱ (i=1,2,3) spécifient complètement un point massique arbitraire ξ. Il convient de noter que l'on emploie partout dans cet article la règle de sommation d'Einstein sur les indices répétés. La position d'un point massique ξ à un moment quelconque t est alors fournie, dans la base non déformée, par x = xⁱ(ξ,t)g_i ou, sous forme vectorielle, par x = x(ξ,t). Cette relation est appelée loi de mouvement du milieu continu, en totale concordance avec la terminologie utilisée pour la mécanique des systèmes de points (discrets). Ainsi, l'approche lagrangienne utilise les quatre variables indépendantes ξ¹, ξ², ξ³, t pour décrire le mouvement, et en particulier la déformation d'un continuum. Par contre, la mécanique de Newton des systèmes de points n'utilise qu'une seule variable indépendante, à savoir le temps t.

Il est essentiel de comprendre que l'idée mathématique derrière la théorie des milieux continus est que le mouvement d'un continuum peut être conçu comme une transformation ponctuelle. En l'absence de phénomènes critiques qui donnent lieu à des singularités, par exemple des transitions de phase, la loi de transformation est bi-univoque, exprimant le fait que deux points massiques différents ne peuvent jamais occuper au même moment le même point de l'espace. Une conséquence en est que le déterminant jacobien est strictement positif, et la loi de mouvement est invertible :

.

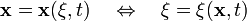
En d'autres termes, tout volume se transforme en un autre volume, toute surface en une autre surface, et toute courbe en une autre courbe. En outre, nous pouvons généralement admettre que deux points massiques appartenant au même continuum qui sont infiniment proches l'un de l'autre à un instant donné resteront infiniment proches l'un de l'autre à l'instant suivant. Ceci implique la continuité des dérivées partielles de x par rapport aux variables ξ¹, ξ², ξ³, t. Selon cette hypothèse de continuité, une quelconque surface fermée reste fermée au cours de la déformation et, de même, une quelconque courbe fermée reste fermée.