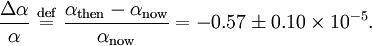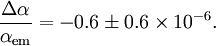Constante de structure fine - Définition

Mesure

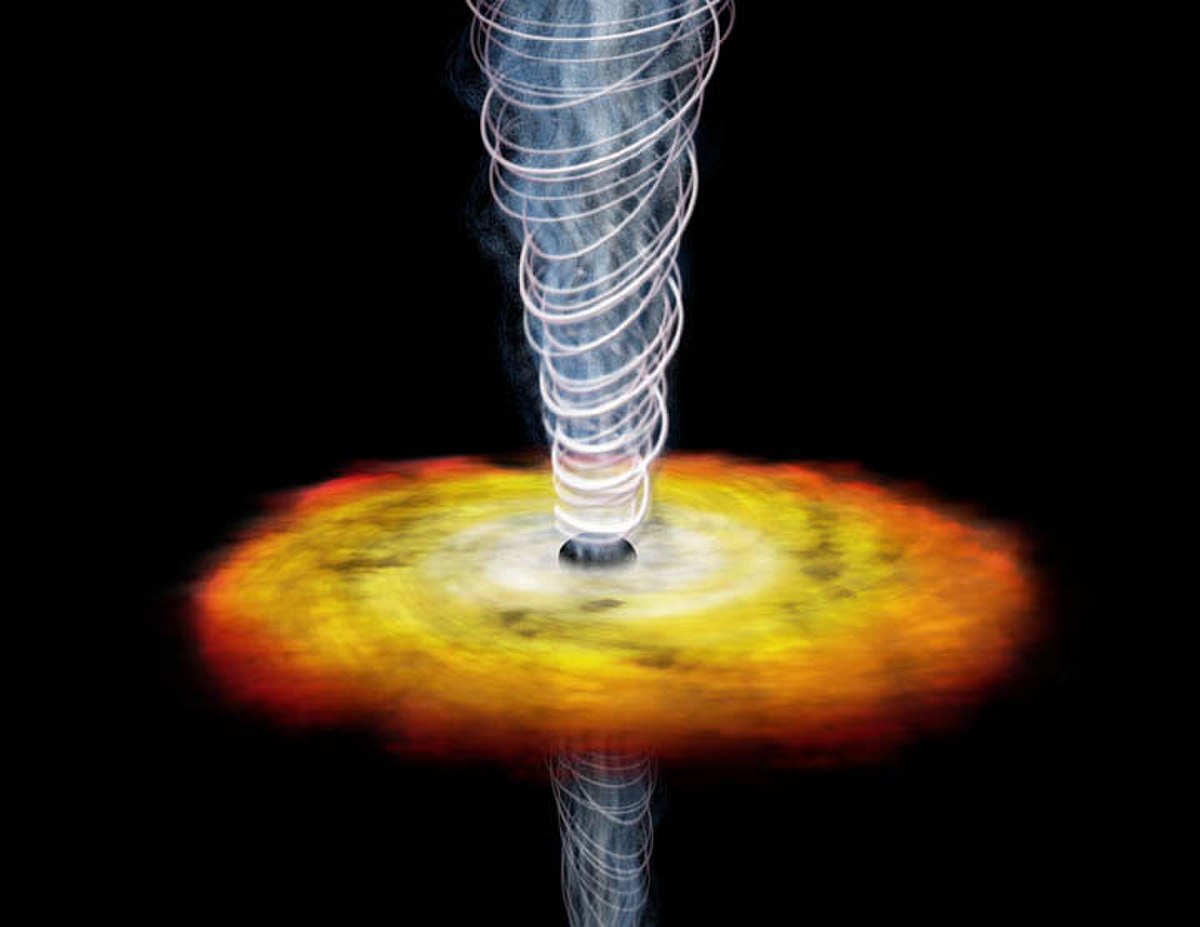
La définition de fait intervenir plusieurs constantes qui peuvent être mesurées indépendamment. Cependant, l'électrodynamique quantique fournit une manière de mesurer directement , en utilisant l'effet Hall quantique ou l'anomalie du moment magnétique de l'électron.

L'électrodynamique quantique (QED) propose une relation entre le moment magnétique de l'électron (autrement dit, le facteur de Landé ) et la constante de structure fine . Une nouvelle mesure de , réalisée par une équipe de l'université d'Harvard en 2006, en utilisant un cyclotron quantique à un électron ainsi que des calculs de QED, impliquant 891 diagrammes de Feynman à 4 boucles, donne l'estimation la plus précise de :

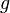
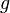
autrement dit une valeur avec une précision de 0.70 ppb. L'incertitude est dix fois plus petite que la meilleure des méthodes concurrentes utilisant les mesures de recul atomique. Les comparaisons entre les valeurs mesurée et calculée de mettent à l'épreuve les théories QED et posent une limite sur la structure interne possible de l'électron.

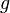
Est-elle réellement constante ?

Les physiciens se demandent si cette constante en est vraiment une, c’est-à-dire si sa valeur ne varie pas avec le temps et suivant la position. Historiquement, il fut proposé un variable pour résoudre les problèmes liés aux observations cosmologiques. Plus récemment, l'intérêt théorique lié à la variabilité des constantes (et pas seulement ) a été motivé par la théorie des cordes et d'autres théories qui vont au-delà du modèle standard de la physique des particules. Les premières expériences qui tentèrent de démontrer cette variabilité, notamment avec l'étude des raies spectrales des objets astronomiques éloignés et la désintégration nucléaire du réacteur nucléaire naturel d'Oklo, ne trouvèrent aucun résultat probant.

Plus récemment, les avancées technologiques ont rendu possible l'évaluation de à une plus grande distance et avec une meilleure précision. En 1999, l'équipe de John K. Webb de l'Université de Nouvelle-Galles du Sud a affirmé avoir détecté une variation de .

Vue d'artiste du quasar GB1508.

En utilisant les Télescopes Keck et une série de données sur 128 quasars avec un décalage vers le rouge de 0,5Webb et al. ont trouvé que les spectres correspondaient à une faible augmentation de sur 10-12 milliards d'années. Plus précisément, il montrèrent que

Une étude plus récente de 23 systèmes absorbants menée par Chand et al. utilise le Very Large Telescope et montre qu'il n'y a aucune variation mesurable :

Le résultat de Chand et al. écarte apparemment la variation avancée par Webb et al., bien qu'il subsiste des incertitudes concernant des erreurs systématiques. Des études complémentaires sont en cours pour obtenir davantage de données. Pour l'instant, tous les autres résultats obtenus confirment la constance de .

Historique

Sommerfeld en 1897.

La constante de structure fine a été introduite pour la première fois en physique en 1916 par Arnold Sommerfeld. Elle mesurait les écarts relativistes entre les raies spectrales atomiques d'après les prédictions du modèle de Bohr.

Historiquement, la première interprétation physique de la constante de structure fine était qu'il s'agissait du rapport entre la célérité de l'électron sur la première orbite circulaire de l'atome de Bohr relativiste et la vitesse de la lumière dans le vide. De façon équivalente, c'était le quotient entre le moment angulaire maximum autorisé par la Relativité pour une orbite fermée et le moment angulaire minimum permis par la mécanique quantique. Elle apparaît dans l'analyse de Sommerfeld et détermine la taille de la séparation de la structure fine des raies spectrales de l'hydrogène.