Critère de Lawson - Définition

Introduction

Le critère de Lawson s'applique à la fusion nucléaire et permet de connaître la rentabilité de la réaction de fusion. Il est nommé en l'honneur de John D. Lawson qui l'a décrit pour la première fois en 1955, dans une note alors classée confidentielle de l'Établissement de recherche atomique d'Harwell (Grande-Bretagne) où il travaillait. L'article fut publié deux ans plus tard dans les Proceedings of the Physical Society.

Formulation du critère

Pour que la fusion soit énergétiquement rentable, il faut que l’énergie produite par les réactions de fusion compense au minimum les pertes inhérentes à la production d'énergie. En pratique, on est amené à considérer la puissance perdue dans le processus, P et la puissance générée par celui-ci, P. Le critère de Lawson stipule simplement que pour que le processus mis en place soit éventuellement rentable, il faut que

P_r > P_perte.

L'inégalité ci-dessus peut ne pas être satisfaite. Dans le bilan énergétique, outre l'énergie produite et l'énergie perdue intervient l'énergie de mise en œuvre.

L'implémentation concrète du critère de Lawson se base sur une estimation de ces deux quantités en fonction du processus considéré.

Pertes et temps de confinement

Sans perte de généralité, lors d'une réaction de fusion nucléaire, les produits de la réaction sont des atomes complètement ionisés baignant dans un gaz d'électrons libres. La densité d'énergie stockée sous forme d'agitation thermique s'écrit selon les lois de la thermodynamique

,

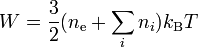
n et les n correspondant respectivement aux concentrations d'électrons et des différentes espèces d'ions, k à la constante de Boltzmann et T à la température à laquelle les réactions sont portées. Ces réactifs se refroidissent spontanément en un temps caractéristique appelé temps de confinement et traditionnellement noté τ. Ce temps dépend du dispositif mis en place pour effectuer les réactions. On a ainsi, par unité de volume,

.

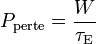
Puissance générée

La puissance par unité de volume générée par les réactions peut s'écrire sous la forme

,

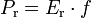
où E désigne l'énergie individuelle générée par une réaction de fusion (soit typiquement quelques MeV), et f le taux de réaction volumique. En supposant que deux espèces nommées 1 et 2 et de concentration n et n réagissent l'une avec l'autre, on a ainsi

,

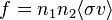
où la quantité nommée <σv> désigne la valeur moyenne du produit de la section efficace de réaction et de la vitesse relative des deux réactifs.

Réécriture du critère de Lawson

Au final, le critère de Lawson peut s'écrire (pour une réaction à deux espèces)

,

ou bien

.

Exemple sur la configuration deutérium-tritium

Dans une configuration de type fusion deutérium-tritium d'abondance identique, on a

,

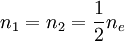
ce qui donne

.

Interprétation physique

Un exemple de la fonction L définie ci-dessus dans le cadre d'une réaction deutérium-tritium.

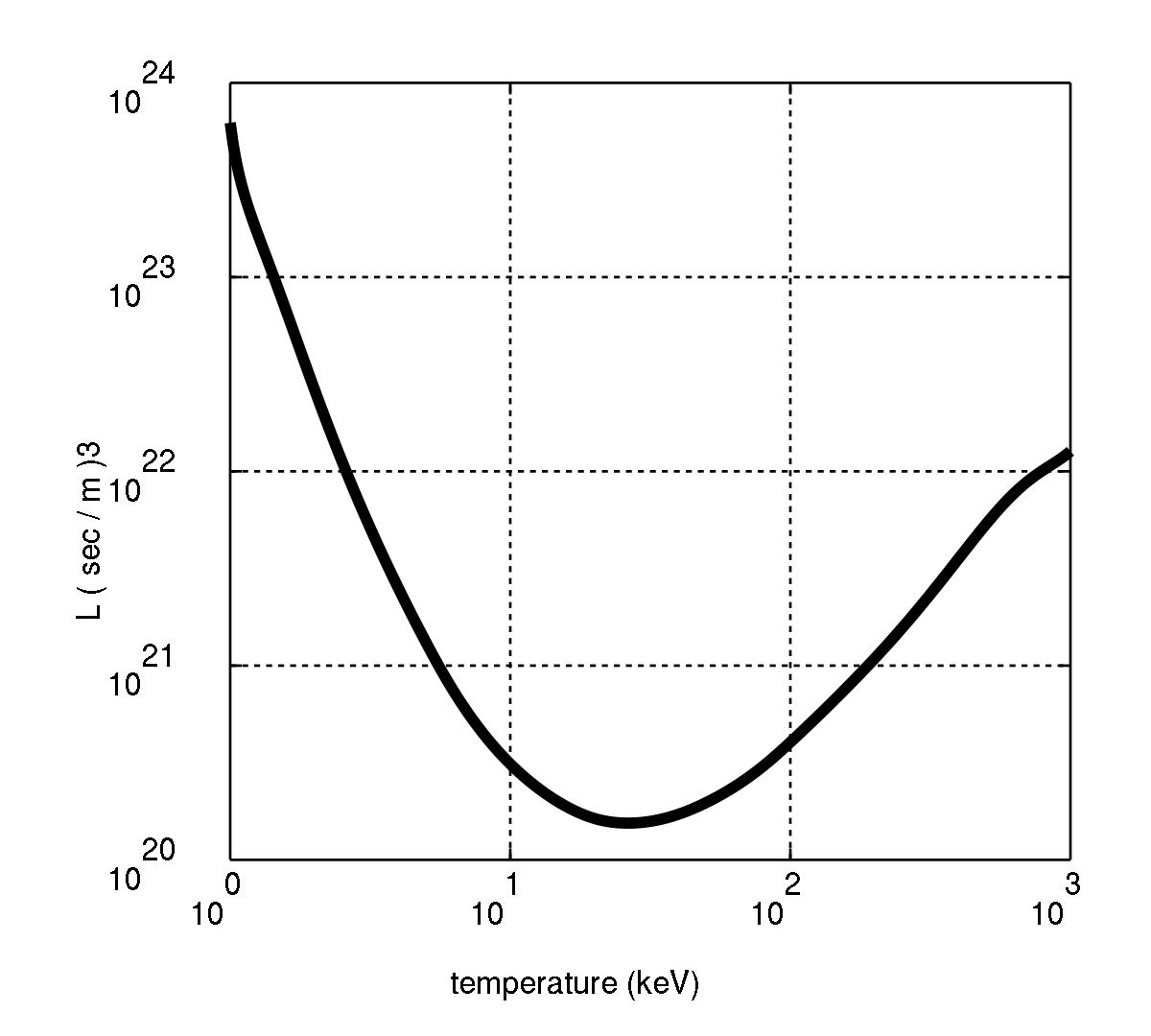
Dans le membre de droite, souvent noté L, toutes les quantités sont uniquement dépendantes de la physique fondamentale du processus de fusion considéré. En particulier, la quantité dépend uniquement de la température et l'on peut en trouver la valeur minimale. Le membre de gauche, lui, dépend du dispositif mis en place pour le réaliser. Ainsi, le critère de Lawson peut-il se réécrire comme une contrainte sur le produit de la concentration des réactifs par le temps de confinement qui doit être supérieur à une valeur fixée par la physique de la réaction.

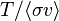
Le fait qu'il soit nécessaire d'avoir le plus grand temps de confinement possible s'interprète par le fait que les pertes d'énergie se font d'autant plus lentement que le temps de confinement est élevé (il est proportionnel à 1/τ). Quant à la nécessité d'avoir la plus grande concentration possible de réactifs, elle s'explique par le fait que le taux de réaction augmente plus vite avec celle-ci que les pertes (respectivement en n² et n).

Prise en compte de l'ensemble du bilan énergétique

La calcul ci-dessus suppose que la totalité de l'énergie de réaction est utilisable. En pratique, cela n'est pas vrai pour deux raisons :

• d'une part, il faut dépenser une certaine quantité d'énergie pour assurer le confinement des réactifs. Cette énergie s'ajoute aux pertes issues de la réaction pour assurer un bilan énergétique positif ;
• d'autre part, seule une partie de l'énergie produite est effectivement récupérable. Par exemple, pour une réaction deutérium-tritium on produit un noyau d'hélium-4 et un neutron. Seule l'énergie du noyau est effectivement récupérable pour le chauffage du plasma.

En pratique, il convient donc d'affecter au critère de Lawson un coefficient correcteur dépendant de ces éléments.