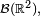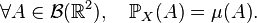Densité de probabilité - Définition
La liste des auteurs de cet article est disponible ici.
Densité de probabilité d'un vecteur aléatoire
Définition — On appelle densité de probabilité d'une variable aléatoire

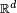

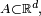
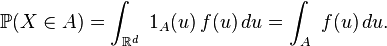
Cette définition est en particulier valable pour
Il existe une définition (équivalente) en termes d'espérance mathématique :
Théorème — Soit une variable aléatoire

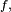

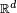
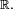
![\mathbb{E}\left[\varphi(X)\right]=\int_{\mathbb{R}^d}\ \varphi(u)\,f(u)\,du](https://static.techno-science.net/illustration/Definitions/autres/c/ccd785562e21d3a6ab16db8a8bdf20bf_bcfdafb0c90148c74270562f1e6c8ddf.png)
a un sens, alors l'autre aussi, et l'égalité a lieu. Réciproquement, si l'égalité ci-dessus a lieu pour tout


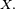
Il existe des variables aléatoires, réelles ou bien à valeurs dans
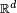
Si une fonction

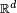
-

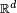
-
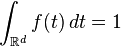
-

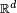
Réciproquement, si une fonction


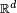

Espérance, variance et moments d'une variable aléatoire réelle à densité
Soit




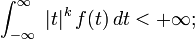
on a dans ce cas
![\mathbb{E}\left[X^k\right] = \int_{-\infty}^{\infty}\ t^k\,f(t)\,dt.](https://static.techno-science.net/illustration/Definitions/autres/2/2d793411128a379757127f8f9cc063c7_056f59db499d859eef7fc9d68ef8915d.png)
En particulier, lorsque le moment d'ordre 2 existe :
![\mathbb{E}\left[X\right] = \int_{-\infty}^{\infty}\ t\,f(t)\,dt,](https://static.techno-science.net/illustration/Definitions/autres/5/5af44a3c8c7ecc1ceb42d0a69ceeb6f1_e6406fe17cb221e96b848ce302aeffb1.png)
![\mathbb{E}\left[X^2\right] = \int_{-\infty}^{\infty}\ t^2\,f(t)\,dt,](https://static.techno-science.net/illustration/Definitions/autres/0/0d7b1bde4c660d72230643eb0eb2307f_2c21e3eb18cd0ab8a5876b3403f6bc38.png)
et, d'après le théorème de König-Huyghens,
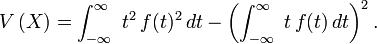
Existence
En vertu du théorème de Radon-Nikodym, le vecteur aléatoire
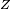
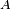
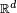
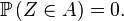
Ce critère est rarement employé dans la pratique pour démontrer que
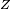
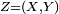
-
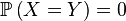
-
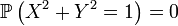
-
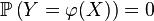
-
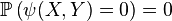
pour des fonctions

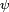
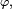
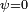
Le critère de Radon-Nikodym peut aussi être utilisé pour démontrer qu'un vecteur aléatoire ne possède pas de densité : par exemple, si
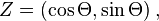
où
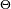
![\scriptstyle\ [0,2\pi]\](https://static.techno-science.net/illustration/Definitions/autres/a/a8259c1af061a0df144341ff223ad533_cdddc2e85124361ab2594b1edb9f1819.png)
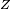
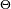
![\scriptstyle\ [0,2\pi]\](https://static.techno-science.net/illustration/Definitions/autres/a/a8259c1af061a0df144341ff223ad533_cdddc2e85124361ab2594b1edb9f1819.png)
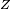
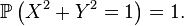
Cas des variables aléatoires réelles à densité
En spécialisant à d=1, on note que, parmi les boréliens
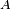
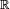
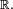
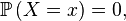
pour tout nombre réel x, et, par conséquent,
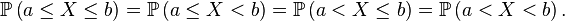
Il suit que les variables aléatoires réelles à densité ont nécessairement une fonction de répartition continue sur
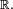
Non-unicité de la densité de probabilité
Si


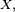


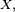
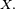

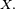
Densité jointe de plusieurs variables aléatoires réelles
La fonction

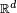
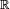
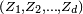

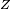
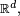
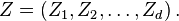
On peut alors calculer la probabilité d'événements concernant les variables aléatoires réelles
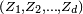
Si
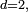
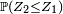
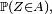
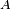
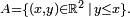
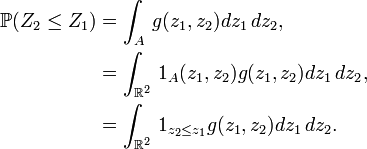
Si par exemple
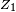
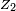
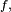
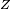
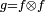
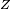

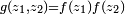
![\begin{align} \mathbb{P}(Z_2\le Z_1) &= \int_{\mathbb{R}^2}\,1_{z_2\le z_1}f(z_1)f(z_2)dz_1\,dz_2, \\ &= \int_{\mathbb{R}}\,\left(\int_{-\infty}^{z_1}f(z_2)\,dz_2\right)f(z_1)dz_1, \\ &= \int_{\mathbb{R}}F(z_1)f(z_1)dz_1 \\ &= \frac12\left[F^2\right]_{-\infty}^{+\infty}=\frac12. \end{align}](https://static.techno-science.net/illustration/Definitions/autres/7/7cc7e8272635c3cc527ee6be298b9486_8fc27320fbb41478ebe567863e6040a1.png)
Si par contre
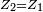
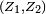
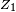
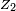

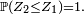
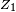
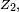
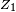
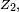
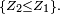
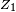
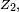
Densité marginale
Soit
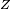
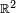
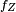
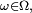
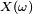
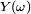
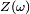
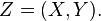
Alors
Propriété — Les variables aléatoires réelles

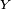
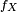
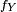
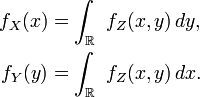
Les densités de probabilités
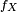
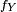
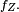
Calculons
![\scriptstyle\ \mathbb{E}\left[\varphi(X)\right],](https://static.techno-science.net/illustration/Definitions/autres/3/3af78e95912638987ebe0ef8bc6507ea_24d2864339b077a3837bcefb00ff331b.png)

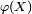
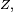
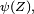
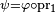
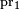
![\begin{align} \mathbb{E}\left[\varphi(X)\right] &= \mathbb{E}\left[\psi(Z)\right] \\ &=\int_{\mathbb{R}^2}\ \psi(z)\,f_Z(z)\,dz \\ &=\int_{\mathbb{R}^2}\ \psi(x,y)\,f_Z(x,y)\,dx\,dy \\ &=\int_{\mathbb{R}}\left(\int_{\mathbb{R}}\ \psi(x,y)\,f_Z(x,y)\,dy\right)\,dx \\ &=\int_{\mathbb{R}}\left(\int_{\mathbb{R}}\ \varphi(x)\,f_Z(x,y)\,dy\right)\,dx \\ &=\int_{\mathbb{R}}\varphi(x)\,\left(\int_{\mathbb{R}}\ f_Z(x,y)\,dy\right)\,dx. \end{align}](https://static.techno-science.net/illustration/Definitions/autres/d/d67ca7aa9d30c0ea980230a2e7103552_56ab7918db11aef3eb924230d2bc3acf.png)
Cela a lieu pour tout

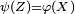
![\scriptstyle\ \mathbb{E}\left[\psi(Z)\right]\](https://static.techno-science.net/illustration/Definitions/autres/2/21e2db74dcb44e591b5227679995520f_9809a9b5d91af1b79eff39cff29e1b91.png)
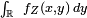
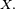
Le cas de
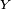
Plus généralement, si

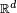
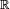
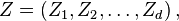
on peut calculer une densité

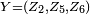
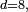
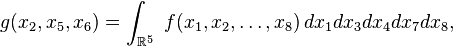
c'est-à-dire en intégrant par rapport à toutes les coordonnées qui ne figurent pas dans le triplet
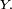

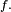
La densité jointe des 9 statistiques d'ordre, notées ici
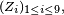
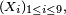
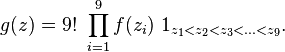
Par définition des statistiques d'ordre, la médiane
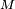
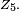
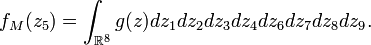
Ainsi, de proche en proche,
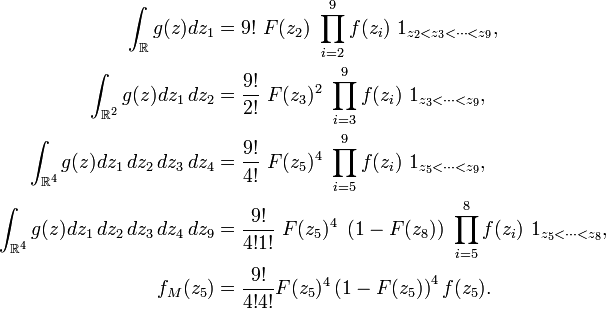
Indépendance des variables aléatoires à densité
Soit une suite
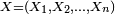
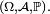
Théorème —
- Si

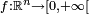
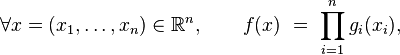
- où les fonctions
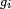

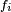
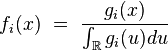
- est une densité de la composante
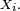
- Réciproquement, si

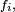


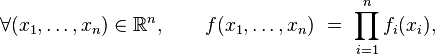
- est une densité de probabilité de
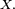
- Sens direct
Comme la densité

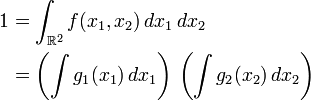
et par suite
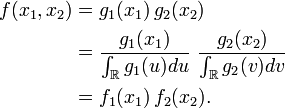
Par construction les fonctions
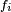
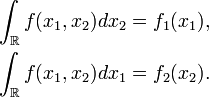
Ainsi les fonctions
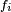
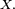

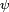
![\begin{align} \operatorname{E}[\varphi(X_1)\psi(X_2)] &= \int \int \varphi(x_1)\psi(x_2)f(x_1,x_2) \, dx_1 \, dx_2\\ &= \int \int \varphi(x_1)f_1(x_1)\psi(x_2)f_2(x_2) \, dx_1 \, dx_2\\ &= \int \varphi(x_1)f_1(x_1) \, dx_1 \int \psi(x_2)f_{2}(x_2) \, dx_2\\ &= \operatorname{E}[\varphi(X_1)] \operatorname{E}[\psi(X_2)]\end{align}](https://static.techno-science.net/illustration/Definitions/autres/a/a8b338883e671d5d74de0cef24cab297_8aa1db279886ec49e28887a2993fcd80.png)
ce qui entraine l'indépendance des variables
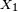
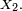
- Sens réciproque
Il suffit de montrer que
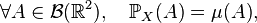
où
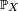
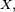

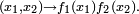
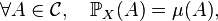
où

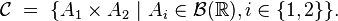
En effet
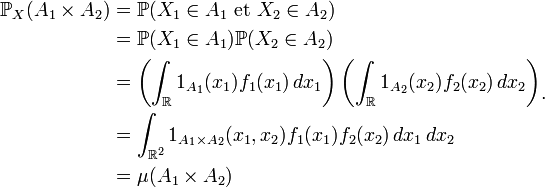
On remarque alors que