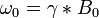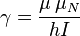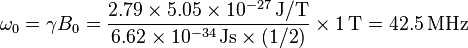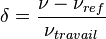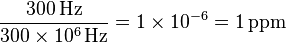Déplacement chimique - Définition

Introduction

En résonance magnétique nucléaire (RMN), le déplacement chimique décrit la dépendance des niveaux d'énergie magnétique du noyau avec l'environnement électronique de la molécule. Les déplacements chimiques sont utilisés dans les techniques de spectroscopie RMN du proton ou du carbone 13 par exemple.
Le noyau d'un atome peut avoir un moment magnétique (spin nucléaire), ce qui donne différents niveaux d'énergie avec une levée de la dégénérescence en présence d'un champ magnétique extérieur.
Le champ magnétique total ressenti par un noyau est la superposition du champ extérieur et du champ local induit par le mouvement des électrons dans les orbitales moléculaires (les électrons ont un moment magnétique propre par ailleurs).

La distribution des électrons pour un même type de noyau (c'est-à-dire 1H, 13C, 15N..) varient selon la géométrie locale (atomes liés, longueurs et angles de liaison) et avec le champ magnétique local de chaque noyaux.
Cela a un impact sur les niveaux d'énergie (et les fréquences de résonance). Les variations des fréquences de résonance magnétique nucléaire d'un même type de noyau, à cause des variations de distributions électroniques, sont appelées « déplacement chimique ».
Le déplacement chimique est donné par rapport à une fréquence de référence ou à un échantillon de référence, souvent une molécule avec une distribution électronique peu déformée.
Le déplacement chimique a une grande importance en spectroscopie RMN, une technique qui explore les propriétés moléculaires par sondage des effets de la résonance magnétique nucléaire.

Fréquence de travail

La fréquence de travail ω₀ d'un aimant est donné par la formule de Larmor.

où B₀ est l'intensité du champ magnétique en teslas ou en gauss, et γ est le rapport gyromagnétique du noyau sondé. Ce rapport est calculé à partir du moment magnétique μ et du spin I avec le magnéton nucléaire μ_N et de la constante de Planck h:

Ainsi la fréquence de travail en RMN 1H et pour un champ de 1 T est calculée :

Le champ magnétique induit

Les électrons autour d'un noyau circulent dans le champ magnétique et créent un deuxième champ magnétique . Ce champ induit s'oppose au champ appliqué comme le stipule la loi de Lenz et le noyau est alors « blindé ». Les variations du déplacement chimique peuvent s'expliquer avec les degrés de blindage ou de déblindage. Par exemple un hydrogène a proximité d'un atome déficient en électrons sera déblindé (champs faibles, déplacement chimique grand).

les noyaux raisonnent dans une large gamme à gauche de la référence (ou plus rarement vers la droite). Quand un signal a lieu pour un plus grand déplacement chimique :

– le champ magnétique appliqué effectivement est plus faible pour une fréquence donnée ;

– la fréquence est plus haute (si le champ extérieur est statique) ;

– le noyau est plus déblindé.

Substance de référence

Le déplacement chimique δ est exprimé habituellement en parties par millions (ppm) et il est calculé de cette manière :

où ν est la fréquence de résonance du noyau sondé, ν_ref celle d'un noyau de référence et ν_travail la fréquence de travail.

En RMN ¹H, ¹³C, et ²⁹Si on utilise habituellement le TMS (tétraméthylsilane) ou le DSS, dont le déplacement chimique est fixé à 0 par convention. D'autres substances sont utilisées comme référence pour les autres noyaux.

Ainsi un signal de RMN à 300 Hz par rapport au TMS avec une fréquence appliquée de 300Mh donne un déplacement chimique de :

Ce mode de calcul permet de s'affranchir du spectromètre utilisé (et de son champ magnétique, différent d'un appareil à l'autre). La fréquence de travail dépend du champ mais pas le déplacement chimique. Le champ magnétique a cependant un impact: il permet une meilleure résolution lorsqu'il est élevé.