Écart type - Définition
La liste des auteurs de cet article est disponible ici.
Estimation
En statistiques, deux estimateurs de l'écart type sont généralement utilisés. Ces estimateurs sont simplement obtenus en prenant la racine des estimateurs de la variance, étant donné que l'écart-type est juste la racine carrée de la variance.
On note très souvent les statistiques variance empirique
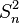
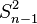
Écart type empirique
Si la valeur exacte de la moyenne
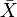
-
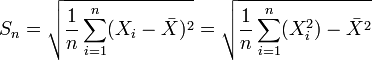
Une réalisation de la statistique S est donnée par:
-
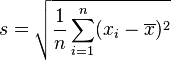
Écart type empirique corrigé
Lorsque la moyenne est une estimation, c'est-à-dire que sa valeur exacte est inconnue (c'est par exemple le cas en physique expérimentale, où l'on n'a accès qu'à la moyenne des valeurs mesurées), l'écart type est donné sous une forme corrigée :
-
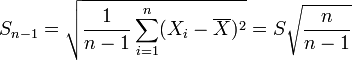
où
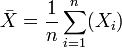
Une réalisation de cette statistique est
-
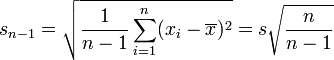
Propriétés des estimateurs
En général, l'estimateur Sn − 1 est préféré, étant donné que l'estimateur
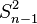
Biais
Pour établir les propriétés des estimateurs de l'écart-type, il est utile de rappeler les propriétés des estimateurs de la variance:
-
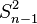
-
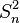
Il n'est cependant pas évident de trouver un estimateur non biaisé de l'écart type. En effet, on sait par l'inégalité de Jensen que:
Inégalité de Jensen — Soit f une fonction convexe sur ]a; b[ et X une variable aléatoire d'espérance finie, à valeurs dans ]a; b[. Alors l'inégalité suivante est vraie :
L'inégalité s'inverse avec des fonctions concaves. Comme la fonction racine carrée est concave, on a:
-
![\operatorname{E}[S^2_{n-1}]=\sigma^2](https://static.techno-science.net/illustration/Definitions/autres/9/9fc2275bc7a8f1bc5100dcdb7d202c95_58f526046ef0fdfd513f2403c3cb19f7.png)
-
![\operatorname{E}\left[\sqrt{S^2_{n-1}}\right]\leq \sqrt{\sigma^2}](https://static.techno-science.net/illustration/Definitions/autres/5/5c89bd1949b3a29a264ba6f28f53d40b_64c507956d74f9c5a7f7ad6d2f795e22.png)
L'estimateur Sn − 1 sera donc biaisé vers le bas.
Il est en fait très difficile d'obtenir un estimateur sans biais, et dans le cas où les données suivent une loi normale la formule est assez complexe, (voir la page anglaise: en:Unbiased estimation of standard deviation).
Convergence
Il est utile de rappeler que:
-
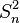
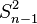
Par le théorème de continuité, on a que :
Théorème — Si g est continue: Si
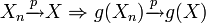
Comme la fonction racine carrée est une fonction continue, Sn − 1 et Sn sont des estimateurs convergents de l'écart-type, soit:
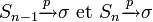
![f(\mathbb{E}(X)) \leq \mathbb{E}[f(X)]](https://static.techno-science.net/illustration/Definitions/autres/1/137134a5624eee429c6948a190da22c6_a983c5563de4e17b88142ac9139d81fd.png)

















































