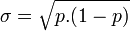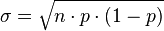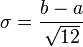Écart type - Définition

Introduction

Représentation graphique d'une loi normale. Chaque bande colorée a la largeur d'un écart type.

En mathématiques, plus précisément en statistiques et probabilités, l'écart type mesure la dispersion d'une série de valeurs autour de leur moyenne.

Dans le domaine des probabilités, l'écart type est une quantité réelle positive, éventuellement infinie, utilisée pour caractériser la répartition d'une variable aléatoire réelle autour de sa moyenne. En particulier, la moyenne et l'écart type caractérisent entièrement les lois gaussiennes à un paramètre réel, de sorte qu'ils sont utilisés pour les paramétrer. Plus généralement, l'écart type, à travers son carré, appelé variance, permet de caractériser des lois gaussiennes en dimension supérieure. Ces considérations ne sont pas sans importance, notamment dans l'application du théorème de la limite centrale.

En statistiques, plus particulièrement en théorie des sondages, ainsi qu'en métrologie, l'écart type tente d'évaluer, à partir d'un échantillon soumis au hasard, la dispersion de la population tout entière. On distingue alors l'écart type empirique (biaisé) et l'écart type empirique corrigé dont la formule diffère de celle utilisée en probabilité.

Les écarts types connaissent de nombreuses applications, tant dans les sondages, qu'en physique (où ils sont souvent nommés RMS (Root Mean Square) par abus de langage), ou en biologie. Ils permettent en pratique de rendre compte des résultats numériques d'une expérience répétée. En finance l'écart type est une mesure de la volatilité d'un actif.

Généralités

En statistiques comme en probabilités on définit, outre des valeurs centrales, des valeurs de dispersion.

Dans le domaine des probabilités, la dispersion d'une variable aléatoire réelle X autour de sa moyenne est caractérisée par la variance dont le calcul repose sur la notion d'espérance mathématique.

Pratiquement, c'est l'écart-type, racine carrée de la variance, qui est utilisé car il possède les mêmes dimensions physiques que la variable. Cette notion apparaît aussi dans l'analyse des signaux, souvent en relation avec la notion de processus aléatoire, généralement sous le nom de moyenne quadratique.

En statistique descriptive qui porte sur une population finie parfaitement connue, les valeurs de dispersion, comme les valeurs centrales, peuvent être choisies arbitrairement (écart-type, écart moyen, étendue, ...).

La statistique mathématique porte au contraire sur une population infinie qui ne peut être connue qu'imparfaitement à travers un ensemble fini de données . Pour interpréter ces données imprécises, il faut faire appel à la notion de probabilité. Les données sont alors considérées comme une réalisation d'un échantillon constitué par les variables aléatoires . Par des calculs arithmétiques analogues à ceux qui sont effectués en statistique descriptive, il est possible de déduire de la réalisation de l'échantillon des estimations de la moyenne empirique et de la variance empirique qui sont elles-mêmes des variables aléatoires. La moyenne empirique fournit une estimation sans biais de la moyenne de la loi de probabilité car son espérance est égale à cette dernière. Au contraire, la variance empirique fournit une estimation biaisée de la variance ; pour obtenir une estimation sans biais, il faut la multiplier par .

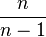
En probabilités

Dans la formulation moderne des probabilités, suite aux travaux de Henri Lebesgue, une variable aléatoire X est une application à valeurs réelles ou vectorielles, dépendant d'un paramètre x suivant une loi de probabilité P. Si la compréhension du formalisme fait appel à la théorie de la mesure, son utilisation reste simple. L'application X ne joue pas un rôle fondamental ; seule sa loi, l'image de P par X, notée P_X, importe. Il s'agit d'une mesure sur R ou sur Rⁿ. Deux quantités lui sont associées :

• Sa moyenne, notée E[X], aussi appelée espérance :
• Son écart type, généralement noté σ_X, défini comme la racine carrée de l'espérance de (X-E[X])² :

.

Ici, l'élévation au carré pour le membre de droite désigne implicitement la norme euclidienne au carré dans le cas où X est à valeurs vectorielles.

Cette identité se spécialise dans un grand nombre de cas particuliers. Entre autres :

Probabilité discrète

Si la variable X prend un nombre fini de valeurs réelles x₁, ..., x_n, avec des probabilités respectives p₁, ..., p_n (sous la condition ), l'écart type est donné par :

, où : .

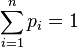
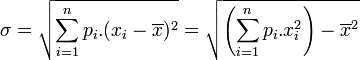
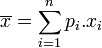
En particulier, si la loi de X est uniforme sur un ensemble fini de valeurs, on a :

, où : .

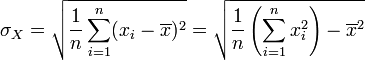
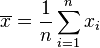
Ces formules se généralisent immédiatement en dimension supérieure en remplaçant l'élévation au carré par la norme euclidienne au carré.

Probabilité uniformément continue

La loi P_X est dite uniformément continue lorsque la probabilité que X appartienne au segment [a, b] est :

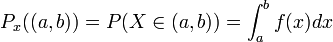
où f est une fonction localement intégrable pour la mesure de Lebesgue, par exemple mais pas nécessairement une fonction continue. Cette fonction f s'appelle la densité de la loi P_X. Elle est globalement intégrable et de carré intégrable.

L'écart type de X est défini par :

.

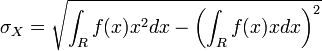
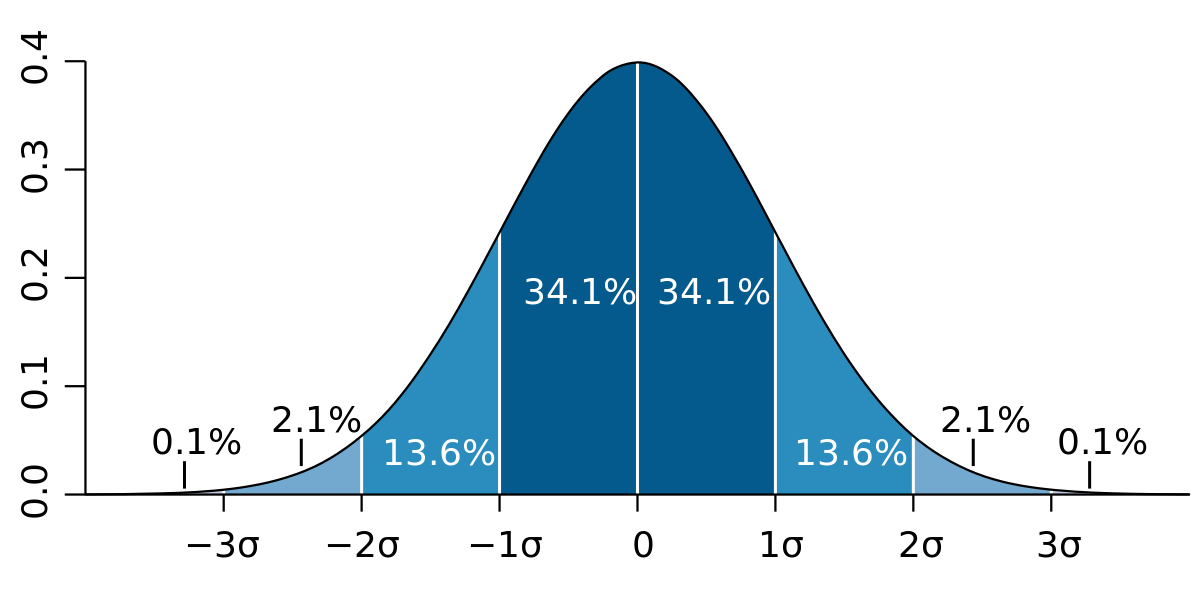
Exemples d'écarts types

Le tableau suivant donne les écarts types pour les lois couramment rencontrées :

Nom de la loi	Paramètre	Description	Ecart-type
Loi de Bernoulli	p	Loi discrète de valeurs 0 avec probabilité 1-p et 1 avec probabilité p
Loi binomiale	p et n>1	Loi de la somme indépendantes de n variables suivant la loi de Bernoulli de paramètre p
Loi géométrique	p	Loi discrète sur N telle que la probabilité d'obtenir l'entier n soit (1-p).pn	σ = p / (1 − p)2
Loi uniforme sur un segment	a<b	Loi uniformément continue sur R de densité la fonction indicatrice de [a, b] à un coefficient près
Loi exponentielle	p	Loi uniformément continue de support R+ de densité la fonction f(x)=p.exp(-p.x)	σ = 1 / p