Équation différentielle stochastique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une équation différentielle stochastique (EDS) est une généralisation de la notion d'équation différentielle prenant en compte un terme de bruit blanc. Les EDS permettent de modéliser des trajectoires aléatoires, tels des cours de bourse ou les mouvements de particules soumises à des phénomènes de diffusion. Elles permettent aussi de traiter théoriquement ou numériquement des problèmes issus de la théorie des équations aux dérivées partielles.
Les domaines d'application des EDS sont vastes : physique, biologie, dynamique des populations, écologie, mathématiques financières, traitement du signal, théorie du contrôle, ...
Quelques approches et définitions informelles
Les EDS comme trajectoires de particules
Le mouvement brownien, nommé ainsi en hommage au botaniste Robert Brown, décrit le mouvement d'une particule soumise à une infinité de chocs en des temps très courts, et ses trajectoires sont erratiques. Elles ont les propriétés suivantes :
- Si l'on connaît la position de la particule à un instant t, alors la loi de sa position spatiale à un instant ultérieur t + s ne dépend que de sa position à cet instant t. Autrement dit, le passé, c'est-à-dire la trajectoire de la particule à des instants antérieurs à t, n'a aucune influence sur ses déplacements futurs. Cette propriété s'appelle la propriété de Markov.
- Les particules bougent continûment dans l'espace.
- La loi de la position de la particule entre deux instants t et t + s ne dépend que de s. Les accroissements sont alors stationnaires.
- En fait, si B(t) désigne la position de la particule à un instant t, alors le loi de B(t) − B(s) et de B(s) − B(r) avec s < r < t sont indépendants l'un de l'autre. Nous dirons alors que les accroissements sont indépendants. En fait, cette propriété implique la propriété de Markov.
- De ces deux derniers faits, et dans l'esprit du théorème central limite, il est alors possible de montrer que B(t) suit une loi normale de moyenne 0 et de variance t.
En d'autres termes, la dynamique de la particule est la même quelle que soit sa position dans l'espace, et si l'on tourne les coordonnées de l'espace à l'aide d'une rotation, un mouvement brownien reste un mouvement brownien : la particule évolue dans un environnement homogène et isotrope.
La notion d'EDS permet de décrire le mouvement d'une particule dans un milieu dont les propriétés physiques peuvent varier, en créant deux effets :
- Si nous connaissons la position X(t) d'une particule, la loi du processus à un instant t + δt est une gaussienne dont la covariance n'est pas nécessairement l'identité, et qui peut dépendre de la position X(t). La covariance doit être de l'ordre de δt.
- En temps très petit, les particules sont poussées dans une direction donnée. Nous parlerons alors de dérive. Cela implique en fait que la position moyenne de la particule à l'instant t + δt sachant la position X(t) est donnée par
![\mathbb{E}[X(t+\delta t)|X(t)]=\mu \delta t](https://static.techno-science.net/illustration/Definitions/autres/8/8c5764dfe550ace6e2aaab7f9b824b06_1070e108dd5f6d38e7ba5b6389af123a.png)
En combinant ces deux effets, nous pouvons écrire
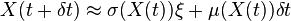
où ξ est une gaussienne normale centrée de covariance l'identité. L'on vérifie facilement que
![\mathbb{E}[X(t+\delta t)|X(t)]=\mu \delta t](https://static.techno-science.net/illustration/Definitions/autres/8/8c5764dfe550ace6e2aaab7f9b824b06_1070e108dd5f6d38e7ba5b6389af123a.png)
et
![\mathbb{E}[(X(t+\delta t)-\mathbb{E}[X(t+\delta t)|X(t)])^2] =\sigma(X(t))\sigma(X(t))^{\mathrm{T}}\delta t](https://static.techno-science.net/illustration/Definitions/autres/3/3083dc55323aaf24e248c8947bfbe255_e3ad0495a6de066ce5c5c63c5b65ef88.png)
En partant de 0, et si l'on somme les accroissements entre kδt et (k + 1)δt, alors nous obtenons
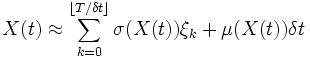
où ne faisons l'hypothèse que les variables gaussiennes ξk sont indépendantes, ce qui est assez raisonnable si nous souhaitons garder la propriété de Markov, c'est-à-dire l'indépendance de la loi des positions futures de la particule après t par rapport aux instant antérieurs à t. Nous pouvons prendre pour ξk les accroissements successifs d'un mouvement brownien.
À l'aide de la théorie des intégrales stochastiques, nous pouvons faire tendre δt vers 0 (attention, il s'agit ici d'une convergence en probabilité !), et considérer l'équation suivante
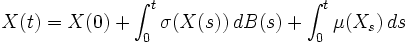
où B est un mouvement brownien, σ est une fonction à valeur matricielle (qui n'est pas forcément une matrice carrée), et μ une fonction à valeur vectorielle. Une telle équation, qui implique donc une intégrale stochastique, est appelée équation différentielle stochastique (EDS).
La théorie des EDS consiste donc à étudier les propriétés de cet objets, et les conditions sur les coefficients qui permettent d'assurer l'existence de tels objets.
Contrairement au mouvement brownien, les solutions d'EDS, sauf dans le cas simple où σ et μ sont constants, ne sont pas à accroissement indépendants et stationnaires. Par contre, elles possèdent bien la propriété de Markov.
Équations différentielles bruitées
Considérons une équation différentielle ordinaire
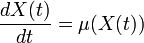
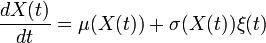
pour une fonction σ. En soi, un bruit blanc est un objet mal défini (cela correspond à un bruit aléatoire où toutes les fréquences sont présentes avec une égale probabilité), et une telle équation n'a pas de sens. Par contre, le bruit blanc étant défini formellement comme la dérivée du mouvement brownien B(t) nous transformons notre équation en
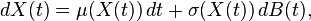
dont nous pouvons prouver qu'elle a bien un sens, à l'aide du calcul stochastique, lorsqu'elle est écrite sous forme intégrale :
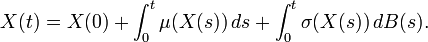
Les EDS comme limites d'équations différentielles ordinaires
Une autre façon naturelle pour considérer les EDS est d'utiliser des interpolations linéaires par morceaux des trajectoires d'un mouvement brownien. Soit B(t,ω) une telle trajectoire, et considérons entre l'instant 0 et l'instant T,
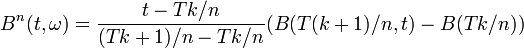
![t\in[Tk/n,T(k+1)/n]](https://static.techno-science.net/illustration/Definitions/autres/7/77957a4dae8fcde6001139a17756da69_28f3fe1d60b42a1c86a77a9e6e9a8d3c.png)
ainsi que les équations différentielles ordinaires (sous de bonnes conditions de régularité sur σ et μ)
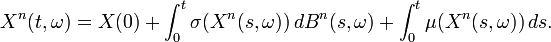
Pouvons-nous montrer que Xn(t,ω) converge quelque chose quand n tend vers l'infini ? En fait, cette approche fonctionne, mais la démonstration n'est pas évidente et comporte des chausses-trappes. En fait, Xn(t,ω) converge vers la solution d'une EDS au sens de Stratonovich
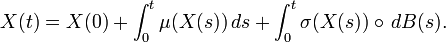
qui implique donc une autre notion d'intégrale stochastique, ici dénotée avec un

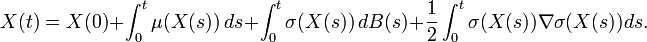
Parmi les difficultés, il convient de noter qu'il est nécessaire, sauf en dimension un, d'utiliser une famille de partition déterministe si l'on souhaite utiliser autre chose qu'une partition régulière, ainsi qu'une interpolation linéaire par morceaux. pour que la convergence vers l'EDS attendue ait bien lieu.

















































