Équation différentielle stochastique - Définition

Lien avec les équations aux dérivées partielles

Équation de Fokker-Planck

U=RxI

Quelques EDS remarquables

Comme pour les équations différentielles ordinaires, nous ne savons pas résoudre une EDS dans le cas général.

Mouvement brownien géométrique

Le mouvement brownien géometrique est un processus de la forme

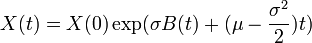
et est couramment utilisé en mathématiques financières pour modéliser l'évolution de cours de bourse (dans le modèle de Black-Scholes) par exemple. Grâce à la formule d'Itô, le mouvement brownien géométrique est solution de

.

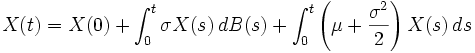
L'équation de Langevin et le processus d'Ornstein-Uhlenbeck

L'équation de Langevin donne le mouvement d'une particule dans un milieu avec friction, et soumise à une force ξ(t) fluctuante (« bain thermique »), que nous prendrons comme un bruit blanc. D'après le principe fondamental de la dynamique, la vitesse de la particule est solution de

.

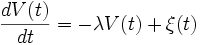
Comme précédemment, cette équation n'a pas vraiment de sens, à moins de la poser sous la forme

,

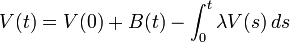
où B(t) est un mouvement brownien. Le paramètre λ spécifie l'intensité de la friction. Cette équation peut être résolue directement :

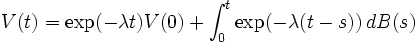
C'est un processus d'Ornstein-Uhlenbeck, et sa particularité est d'être un processus gaussien. Sa moyenne et sa variance sont

et .

Notons qu'ici, nous avons considéré la vitesse de la particule. Sa position est donnée par , et est en soi une trajectoire régulière, mais qui reste un processus gaussien.

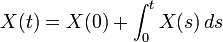
En faisant tendre certains paramètres vers l'infini, alors nous pouvons approcher X(t) par une EDS

Particule aléatoire dans un champ de force

Nous pouvons raffiner l'équation de Langevin en ajoutant un champ de force qui dépend de la position. Alors la position et la vitesse de la particule sont solutions d' une équation que nous écrirons sous la forme

où λK est le champ de force considéré, et λ,D > 0. Il est alors possible de montrer que la position X(t), lorsque λ tend vers l'infini, se comporte elle-même comme la solution de l'EDS

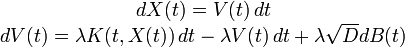
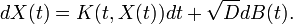
En application, si U est un potentiel, c'est-à-dire que son gradient est une force, alors

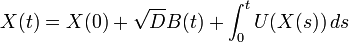
est une EDS couramment utilisée en physique. Sans la présence du mouvement brownien dans le modèle précédent, la particule sera immobilisée au fond des puits de U, c'est-à-dire là où le gradient est nul. En présence d'un bruit, même petit, elle a alors la possibilité de s'échapper et de passer d'un puits à l'autre, et de telles dynamiques sont souvent étudiées (on a parfois des phénomènes de résonance stochastique).

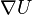
Pont brownien

La probabilité qu'un mouvement brownien atteigne un point donné à un temps fixé T est nulle. Cependant, on a parfois besoin de considérer la trajectoire d'un mouvement brownien (ici en une dimension) conditionnée par un tel événement. On peut construire un tel objet X(t) comme la solution de

Les trajectoires de X(t) partiront de a et atteindront le point b au temps T. Le processus X est un processus gaussien.

Domaines d'applications

• modélisation de phénomènes de diffusion en physique (mécanique des fluides, géophysique, ...) : c'est à l'origine de la motivation de l'étude du mouvement brownien ;

• dynamique des populations, écologie, ... : modélisation de la localisation de la population d'une espèce donnée, ou encore de sa taille...

• méthodes de Monte-Carlo : résolution de certaines équations aux dérivées partielles par des méthodes aléatoires ;

• mathématiques financières : modélisation des cours de bourse ;

• théorie du contrôle stochastique : il s'agit de trouver des stratégies permettant de minimiser ou maximiser certaines quantités soumises à des fluctuations aléatoires mais spécifiées par des paramètres que l'on peut faire varier (valeur d'un portefeuille d'actions, régulation du débit d'un barrage, ...) ;

• systèmes dynamiques aléatoires ;

• résonance stochastique, modélisation en neuroscience, climatologie (des modèles de climat sur de très longues périodes utilisent des EDS).

• modèles d'écoulements de polymères multi-échelles