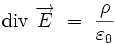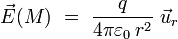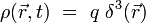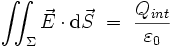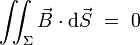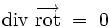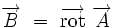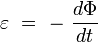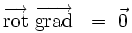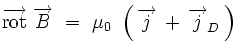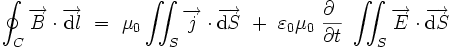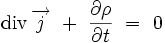Équations de Maxwell - Définition

Théorie de Maxwell-Lorentz dans le vide

On présente ci-dessous la théorie microscopique fondamentale qui donne les équations de Maxwell-Lorentz dans le vide en présence de sources, qui peuvent être des charges ponctuelles et/ou leurs courants électriques microscopiques associés si ces charges sont en mouvement dans le référentiel d'étude.

La théorie macroscopique nécessitant l'introduction des champs D et H (et les équations de Maxwell associées) est discutée en détail dans Électrodynamique des milieux continus.

On note :

• la densité volumique de charge électrique au point à l'instant t.
• le vecteur densité de courant.
• le vecteur champ électrique.
• le pseudo-vecteur induction magnétique.
• la permittivité diélectrique du vide.
• la perméabilité magnétique du vide.

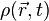
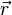
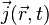
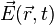
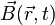
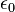
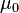
Équation de Maxwell-Gauss

L'équation locale de Maxwell

Cette équation locale donne la divergence du champ électrique en fonction de la densité de la charge électrique :

Cette équation correspond à un « terme de source » : la densité de charge électrique est une source du champ électrique. Par exemple, pour une charge ponctuelle fixée à l'origine , la loi de Coulomb donnant le champ électrostatique en un point de l'espace, point repéré par le vecteur position où est le vecteur unitaire radial, s'écrit :

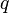
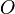
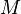
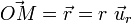
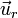
Ce champ électrostatique vérifie l'équation de Maxwell-Gauss pour la source statique :

où est la distribution de Dirac dans l'espace à trois dimensions.

Le théorème de Gauss

L'équation de Maxwell-Gauss est héritée du théorème de Gauss, qui permet de lier le flux du champ électrique à travers une surface fermée à la charge intérieure à cette surface :

où est une surface fermée arbitraire, appelée surface de Gauss, et la charge électrique totale intérieure à cette surface .

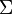
On remarquera que l'équation de Maxwell-Gauss se retrouve facilement en appliquant le théorème d'Ostrogradski au théorème de Gauss et en prenant un volume infinitésimal.

Équation de Maxwell de conservation du flux (Équation de Maxwell-Thomson)

Le flux du champ magnétique à travers une surface fermée est toujours nul :

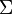
L'équation locale de Maxwell

Cette équation locale est au champ magnétique ce que l'équation de Maxwell-Gauss est au champ électrique, à savoir une équation avec « terme de source », ici identiquement nul :

Elle traduit le fait expérimental suivant : il n'existe pas de monopôle magnétique. Un monopôle magnétique serait une source ponctuelle de champ magnétique, analogue de la charge électrique ponctuelle pour le champ électrique. Or, l'objet de base source d'un champ magnétique est l'aimant, qui se comporte comme un dipôle magnétique : un aimant possède en effet un pôle nord et un pôle sud. L'expérience fondamentale consistant à tenter de couper un aimant en deux donne naissance à deux aimants, et non un pôle nord et un pôle sud séparément.

Introduction du potentiel-vecteur

L'analyse vectorielle montre que la divergence d'un rotationnel est toujours identiquement nulle :

Réciproquement, tout champ de vecteurs dont la divergence est identiquement nulle peut localement être exprimé sous la forme d'un rotationnel.

L'équation locale de conservation du flux magnétique permet donc de définir au moins localement un potentiel-vecteur tel que :

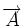
Le problème important de l'unicité du potentiel-vecteur est discuté dans l'article Invariance de jauge de la théorie.

Équation de Maxwell-Faraday

Cette équation locale traduit le phénomène fondamental d'induction électromagnétique découvert par Faraday.

L'équation locale

Elle donne le rotationnel du champ électrique en fonction de la dérivée temporelle du champ magnétique :

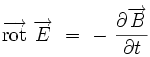
Cela correspond à un « terme variationnel » : la variation du champ magnétique crée un champ électrique. Sa forme intégrale est la loi de Faraday :

où , est la force électromotrice d'induction dans un circuit électrique et le flux magnétique à travers ce circuit.

Introduction du potentiel électrique

L'analyse vectorielle montre que le rotationnel d'un gradient est toujours identiquement nul :

L'équation de Maxwell-Faraday couplée à l'existence locale d'un potentiel-vecteur permettent de définir (au moins localement) le potentiel électrique (scalaire) tel que :

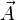
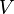
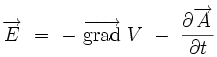
Le problème important de l'unicité du potentiel électrique est discuté dans Invariance de jauge de la théorie.

Équation de Maxwell-Ampère

L'équation locale de Maxwell

Cette équation est héritée du théorème d'Ampère. Sous forme locale, elle s'écrit en termes du vecteur densité de courant  :

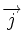
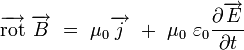
Introduction du courant de déplacement

L'équation précédente peut se réécrire :

en introduisant le courant de déplacement de Maxwell :

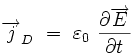
La forme intégrale lie la circulation du champ magnétique sur un contour C fermé, et les courants qui traversent la surface s'appuyant sur ce contour :

Équation de conservation de la charge

Prenons la divergence de l'équation de Maxwell-Ampère :

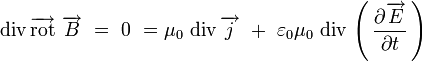
On peut écrire en permutant les dérivées spatiales et temporelles, puis en utilisant l'équation de Maxwell-Gauss :

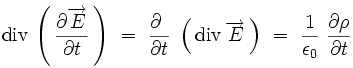
On obtient finalement l'équation locale de conservation de la charge électrique :

La présence du terme de courant de déplacement, introduit par Maxwell, est essentielle à l'obtention de cette équation.