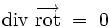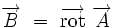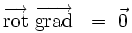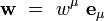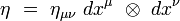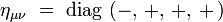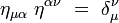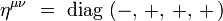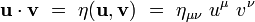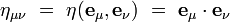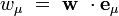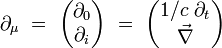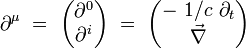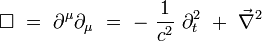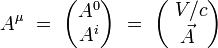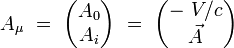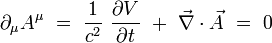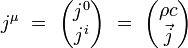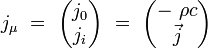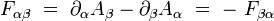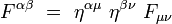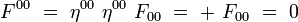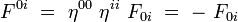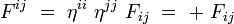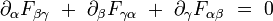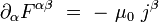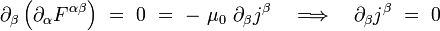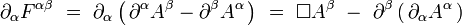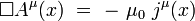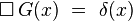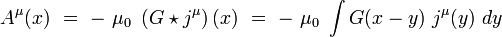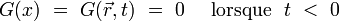Équations de Maxwell - Définition
La liste des auteurs de cet article est disponible ici.
Invariance de jauge de la théorie
L'analyse vectorielle montre que la divergence d'un rotationnel est toujours identiquement nulle :
|
|
L'équation locale de conservation du flux magnétique permet donc de définir au moins localement un potentiel-vecteur
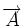
|
|
L'analyse vectorielle nous dit également que
|
|
Alors le potentiel-vecteur n'est pas défini de manière unique puisque la transformation suivante, avec

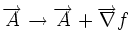
ne modifie par la valeur du champ
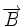
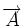
Le lecteur notera qu'en physique classique, le potentiel-vecteur semble n'être qu'un outil mathématique commode pour analyser les solutions des équations de Maxwell, mais ne semble pas être une grandeur physique directement mesurable. En 1959, dans le cadre de la physique quantique, Aharonov et Bohm ont démontré que le potentiel-vecteur avait un effet observable en mécanique quantique : c'est l'effet Aharonov-Bohm.
L'analyse vectorielle montre que le rotationnel d'un gradient est toujours identiquement nul :
|
|
L'équation de Maxwell-Faraday couplée à l'existence locale d'un potentiel-vecteur
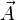
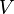
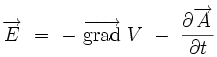
|
Le potentiel
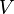
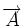
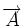
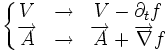
Ces deux équations donnent l'invariance de jauge complète des équations de Maxwell.
Formulation covariante
NB Cette partie suit les conventions de signe classiques de MTW
Cette partie adopte également la convention de sommation d'Einstein.
Géométrie de l'espace-temps de Minkowski
L'espace-temps de Minkowski (1908) est une variété différentielle M plate munie d'une métrique lorentzienne.
Soit un système de coordonnées quelconque xμ autour d'un évènement (point) P de l'espace-temps, et soient
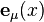
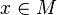
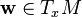
|
|
Les wμ sont appelée les composantes contravariantes du vecteur w. Le tenseur métrique
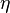
|
|
Dans une base orthonormée d'un référentiel inertiel, ses composantes covariantes ημν sont :
|
|
Ses composantes contravariantes ημν vérifient :
|
|
On obtient explicitement :
|
|
On utilisera ci-dessous les conventions usuelles suivantes :
- un indice grec varie de 0 à 3. Il est associé à une grandeur dans l'espace-temps.
- un indice latin varie de 1 à 3. Il est associé aux composantes spatiales d'une grandeur dans l'espace-temps.
Par exemple, les composantes contravariantes du 4-vecteur position s'écrivent dans un système de coordonnées orthonormales :
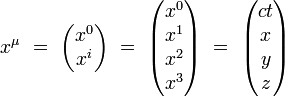
|
Le tenseur métrique définit pour chaque point
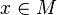
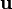
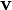
|
|
En particulier, en prenant deux vecteurs de base, on obtient les composantes :
|
|
wμ désignant les composantes contravariantes du vecteur w, on peut définir de même ses composantes covariantes par :
|
|
Par exemple, les composantes covariantes du 4-vecteur position s'écrivent dans un système de coordonnées orthonormales :
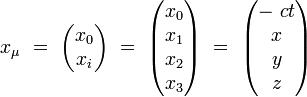
|
Quadri-gradient
On introduit l'opérateur différentiel quadri-gradient par ses composantes covariantes :
|
|
Ses composantes contravariantes s'écrivent :
|
|
L'opérateur invariant d'Alembertien s'écrit par exemple :
|
|
Quadri-potentiel
On introduit le quadri-potentiel électromagnétique par ses composantes contravariantes :
|
|
où V est le scalaire potentiel électrique, et
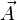
|
|
Les lois de transformation de jauge écrite précédemment sont donc résumées dans cette notation sous la forme
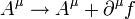
La condition de jauge de Lorenz s'écrit par exemple de façon covariante :
|
|
Quadri-courant
On introduit le quadri-courant électromagnétique par ses composantes contravariantes :
|
|
où ρ est le scalaire densité électrique de charge, et
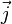
|
|
Tenseur de Maxwell
Le tenseur électromagnétique est le tenseur anti-symétrique de rang deux défini à partir du quadri-potentiel par :
|
|
Ses composantes covariantes s'écrivent explicitement :
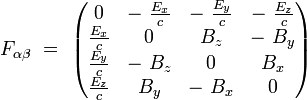
|
On obtient ses composantes contravariantes en écrivant :
|
|
La métrique étant diagonale dans un référentiel inertiel, on obtient alors les formules suivantes, sans sommation sur les indices répétés :
soit explicitement :
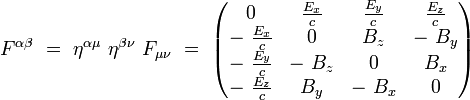
|
Équations de Maxwell sous forme covariante
Les équations de Maxwell se mettent sous forme relativiste covariante.
- Les deux équations de Maxwell sans termes de sources s'écrivent :
|
|
- Les deux équations de Maxwell avec termes de sources s'écrivent :
|
|
Puisque le tenseur de Maxwell est anti-symétrique, cette dernière relation entraîne en particulier que le quadri-courant est conservé :
|
|
Équation de propagation pour le quadri-potentiel en jauge de Lorenz
En écrivant explicitement le tenseur de Maxwell en termes du quadri-potentiel dans l'équation covariante avec terme de sources, on obtient pour le membre de gauche :
|
|
Dans la jauge de Lorenz
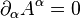
|
|
La solution de cette équation s'écrit de façon simple si l'on connaît une fonction de Green de l'équation de propagation, c'est-à-dire une fonction G(x) solution de l'équation aux dérivées partielles :
|
|
où δ(x) est la distribution de Dirac. On obtient alors le quadri-potentiel sous la forme d'un produit de convolution :
|
|
Exemple : les potentiels retardés
En électrodynamique classique, on utilise le plus souvent la fonction de Green retardée qui satisfait à l'hypothèse de causalité :
|
|