Étoile à neutrons - Définition
La liste des auteurs de cet article est disponible ici.
Structure interne
La croûte
La croûte d'une étoile à neutrons correspond à la région principalement composée de noyaux atomiques.
État fondamental de la matière dense (croûte externe)
Un aperçu de la structure de la croûte peut être donné en calculant l'état de plus basse énergie de la matière à haute pression. Tant que celle-ci n'est pas trop élevée (voir ci-dessous), l'état le plus stable est a priori un cristal de noyaux atomiques tous identiques. Sous sa forme la plus compacte, le cristal est de type cubique centré. On sait qu'à pression nulle, ce cristal est composé de noyaux de fer-56 (c'est-à-dire composé de 26 protons et 30 neutrons). Leur masse volumique est de 7,86 grammes par centimètre cube. À mesure que l'on augmente la pression la composition du noyau le plus stable est susceptible de changer, principalement pour la raison suivante : si l'on considère une maille élémentaire du cristal, celui-ci contient un noyau, possédant Z protons et A nucléons, ainsi que Z électrons (pas nécessairement liés au noyau, celui-ci étant susceptible d'être ionisé), alors l'équation donnant le potentiel chimique μ d'un des A nucléons s'écrit
- Aμ = W(A,Z) + Zμe,
μ étant le potentiel chimique des électrons et W l'énergie de noyau, incluant son énergie de masse et son énergie de liaison. Cette équation se réécrit
-
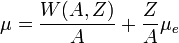
Les électrons vont assez vite ne plus être liés aux noyaux : les électrons étant des fermions, le nombre de ceux-ci ayant une basse énergie est limité, et la pression aidant, la quasi-totalité d'entre eux acquièrent une énergie suffisante pour ne plus être liés au noyau. Les électrons se comportent ainsi comme un gaz de Fermi. Dans un tel gaz, la dépendance du potentiel chimique avec la pression P est connue, en l'occurrence on a
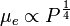
La difficulté de la méthode ci-dessus réside dans celle du calcul de l'énergie W du noyau. Celle-ci peut être obtenue expérimentalement pour des noyaux pas trop instables, mais nécessite au bout d'un moment de faire appel à l'extrapolation de formules établies, ou alors à des calculs complexes de physique nucléaire. Doit en particulier être pris en compte le fait qu'un noyau atomique peut être décrit par un formalisme appelé modèle en couches, qui révèle que certaines valeurs pour le nombre de protons et de neutrons, appelées nombres magiques confèrent une meilleure stabilité aux noyaux, à l'instar des atomes qui sont chimiquement plus stables quand ils comportent un certain nombre d'électrons (c'est la fameuse série de gaz rares, avec dans l'ordre 2, 10, 18, 26, 54, 86 électrons pour respectivement l'hélium, le néon, l'argon, le krypton et le radon). En physique nucléaire, les nombres magiques sont 2, 8, 20, 28, 50, 82, 126. Il existe également des « sous-couches » relativement stables, notamment celle à 40 neutrons ou protons. Les calculs de la configuration la plus stable des noyaux remonte à 1971, avec un travail désormais classique de Gordon Baym, Christopher Pethick et Peter Sutherland, et a été amélioré par la suite par Pawel Haensel et ses collaborateurs. Les calculs révèlent ainsi qu'à partir d'une masse volumique de 7,96×106 grammes par centimètre cube, l'état le plus stable est d'abord composé de noyaux de nickel, à 28 protons (un des nombres magiques). Ces noyaux de nickel ont au départ 62 nucléons (soit 34 neutrons), et s'enrichissent de 2, puis quatre neutrons supplémentaire (nickel-66). Passé 1,49×109 g·cm-3, l'état le plus stable est formé de noyaux à 50 neutrons, s'appauvrissant progressivement en protons, allant du krypton-86 (36 protons) au nickel-78 (28 protons, ce noyau est stabilisé par le fait que le nombre de neutrons et protons est à chaque fois un nombre magique). Ce noyau est le plus neutronisé à avoir été obtenu en laboratoire. La suite des prédictions, quand la masse volumique dépasse les 9,64×1010 g·cm-3 est plus incertaine, en l'absence de données expérimentales. Il semble que le nouvel état le plus stable fasse appel à des noyaux à 82 neutrons, s'appauvrissant progressivement en protons. Le premier de la liste est le rubidium-126 (44 protons et 82 neutrons), et le dernier le krypton-118 (36 protons et 82 neutrons). Les incertitudes sur cette dernière partie sont non négligeables, Pawel Haensel ayant fait remarquer qu'il était possible que ce soit une configuration avec une sous-couche de 40 protons (zirconium) qui soit préférée.
Le tableau ci-dessous résume la succession des noyaux supposés les plus stables à mesure que la densité de la matière augmente.
| Élément et nombre de nucléons (A) | Nombre de protons (Z) | Nombre de neutrons (N) | Z / A | Masse volumique maximale (g·cm-3) | Saut en densité par rapport à l'état précédent (%) |
|---|---|---|---|---|---|
| Fe-56 | 26 | 30 | 0,4643 | 7,96×106 | - |
| Ni-62 | 28 | 34 | 0,4516 | 2,71×108 | 2,9 |
| Ni-64 | 28 | 36 | 0,4375 | 1,30×109 | 3,1 |
| Ni-66 | 28 | 38 | 0,4242 | 1,48×109 | 3,1 |
| Kr-86 | 36 | 50 | 0,4186 | 3,12×109 | 2,0 |
| Se-84 | 34 | 50 | 0,4048 | 1,10×1010 | 3,3 |
| Ge-82 | 32 | 50 | 0,3902 | 2,80×1010 | 3,6 |
| Zn-80 | 30 | 50 | 0,3750 | 5,44×1010 | 3,9 |
| Ni-78 | 28 | 50 | 0,3590 | 9,64×1010 | 4,3 |
| Ru-126 | 44 | 82 | 0,3492 | 1,29×1011 | 4,0 |
| Mo-124 | 42 | 82 | 0,3387 | 1,88×1011 | 3,0 |
| Zr-122 | 40 | 82 | 0,3279 | 2,67×1011 | 3,2 |
| Sr-120 | 38 | 82 | 0,3167 | 3,79×1011 | 3,4 |
| Kr-118 | 36 | 82 | 0,3051 | 4,33×1011 | 3,6 |
Ce type de structure cristalline existe jusqu'à environ 4,33×1011 g·cm-3, moment où l'état le plus stable n'est plus un cristal de noyaux baignant dans un liquide d'électrons, mais un mélange noyau-neutrons libres-électrons. Cette transition est traditionnellement appelé point de fuite neutronique, car c'est le moment où il devient thermodynamiquement avantageux pour les neutrons de diffuser en dehors des noyaux.

















































