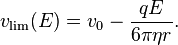Expérience de la goutte d'huile de Millikan - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L’expérience de la goutte d’huile Millikan (Université de Chicago, début du XXe siècle) consiste à pulvériser de minuscules gouttes d’huiles électrisées entre les deux électrodes horizontales d'un condensateur plan chargé. Les minuscules gouttes subissent plusieurs forces qui s'équilibrent rapidement et font que chaque goutte se déplace à vitesse constante mesurable avec une lunette de visée et un chronomètre.
L'expérience consiste à sélectionner une gouttelette et à analyser son mouvement sous l'action des forces agissant sur elle à différentes valeurs d'ionisation :
- son poids vers le bas qui est constant ;
- la poussée d’Archimède (puisque entre les électrodes, il y a de l'air) qui est constante ;
- la force électrostatique vers le haut proportionnelle à sa charge électrique, et qui est proportionnelle au champ et constante dans un champ uniforme ;
- la résultante de ces trois forces est donc constante et est très rapidement compensée par le frottement avec l’air ce qui conduit à observer un mouvement de la gouttelette à vitesse limite constante puisque la somme des forces agissantes est nulle.
Millikan, par simple mesure de vitesse par le rapport de la distance parcourue sur le temps mis pour la parcourir sur une gouttelette d'huile qu'il ionisait en l'irradiant par rayons X, observa expérimentalement que les valeurs d'ionisation étaient toutes multiples entières de e=1,592×10−19 C, constante que l’on connaît aujourd’hui sous le nom de charge élémentaire (avec une valeur mise à jour légèrement différente : e=1,60217646×10−19 C) et que l’on note traditionnellement e ; cette expérience s'est avérée être la première preuve de la quantification de la charge électrique qui est strictement toujours un multiple entier positif ou négatif de cette valeur fondamentale e.
Cette expérience et ses conclusions sur la quantification des charges valurent à Millikan le Prix Nobel de physique en 1923.
Mise en œuvre
On pulvérise des gouttes d’huile entre deux armatures métalliques (condensateur plan) entre lesquelles règne un champ électrique uniforme. La variation du potentiel permet de maîtriser la vitesse des gouttes si celles-ci sont chargées jusqu’à les immobiliser si nécessaire, voire d’inverser leur course. On observe les gouttelettes avec une lunette de visée de façon à mesurer à l’aide d'un micromètre étalonné la distance parcourue et à l'aide d'un chronomètre le temps correspondant: on en déduit la vitesse de la gouttelette sélectionnée. Millikan utilisa un système optique composé d'un objectif de focale 12,5 cm et un oculaire ayant une focale de 12 mm, l'objectif étant à 25 cm de distance de la goutte; l'oculaire comporte un réticule gradué étalonné à l'aide d'un micromètre gradué positionné à 25 cm. On utilise des huiles à basse pression de vapeur afin d’éviter que les gouttelettes ne s’évaporent sous la chaleur de l’éclairage, ce qui fausserait les résultats par une variation de la masse de la gouttelette au cours de l’expérience. Les gouttes peuvent être chargées par simple frottement avec le gicleur du vaporisateur ou tout autre mécanisme d'électrification. Millikan utilisa des rayons X. Une autre précaution à prendre est de ne pas être perturbé par des phénomènes de convection.
Théorie
Dans le cas d’une modélisation simple, une gouttelette d’huile est soumise à quatre forces :
- son poids :
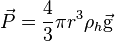
- la force électrostatique :
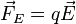
- la poussée d'Archimède :
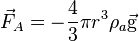
- la force de traînée (résistance de l’air) dont l'expression la plus simple est probablement la loi de Stokes :
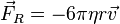
Le principe fondamental de la dynamique sur un axe vertical donne donc :
En supposant une vitesse initiale nulle, la solution de l'équation donne :
On pose
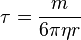
Autrement dit, la gouttelette atteint très vite une vitesse limite ne dépendant plus du temps qui a pour valeur :
Soit v0 = vlim(0) la vitesse à champ nul. On peut alors réécrire
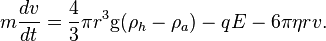
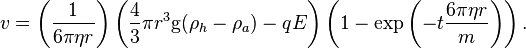
![v_\text{lim}(E) = \left( \frac{1}{6 \pi \eta r} \right) \left[ \frac{4}{3} \pi r^3 \mathrm{g} (\rho_h - \rho_a)- q E \right] .](https://static.techno-science.net/illustration/Definitions/autres/b/beed5c8f9ed51d9ca0100c560c88e667_12ba0cfa77d9f6b0b3fe5c306aabd066.png)