Filtre passe-bas - Définition

Introduction

Un filtre passe-bas est un filtre qui laisse passer les basses fréquences et qui atténue les hautes fréquences, c'est-à-dire les fréquences supérieures à la fréquence de coupure. Il pourrait également être appelé filtre coupe-haut. Le filtre passe-bas est l'inverse du filtre passe-haut et ces deux filtres combinés forment un filtre passe-bande.

Le concept de filtre passe-bas est une transformation mathématique appliquée à des données (un signal). L'implémentation d'un filtre passe-bas peut se faire numériquement ou avec des composants électroniques. Cette transformation a pour fonction d'atténuer les fréquences supérieures à sa fréquence de coupure f_c et ce, dans le but de conserver uniquement les basses fréquences. La fréquence de coupure du filtre est la fréquence séparant les deux modes de fonctionnement idéaux du filtre : passant ou bloquant.

Filtre idéal

Un filtre passe-bas idéal a un gain constant dans sa bande passante et un gain nul dans la bande coupée. La transition entre les deux états est instantanée. Mathématiquement, il peut être réalisé en multipliant le signal par une fenêtre rectangulaire dans le domaine fréquentiel ou par une convolution avec un sinus cardinal (sinc) dans le domaine temporel. Ce type de filtre est appelé « mur de brique » dans le jargon des ingénieurs.

Naturellement, un filtre idéal n'est pratiquement pas réalisable, car un sinus cardinal est une fonction infinie. Ainsi, le filtre devrait prédire le futur et avoir une connaissance infinie du passé pour effectuer la convolution et obtenir l'effet désiré. Il est possible d'approximer très fidèlement ce filtre de manière numérique lorsqu'on dispose d'un signal pré-enregistré (en ajoutant des zéros aux deux extrémités de la série d'échantillons) ou pour un signal périodique.

En temps réel, les filtres numériques peuvent approximer ce filtre en insérant un délai volontaire dans le signal, ce qui permet de « connaître le futur du signal ». Cette opération crée un déphasage entre la sortie et l'entrée et naturellement, plus le délai inséré est court, plus le filtre se rapprochera du filtre idéal.

Filtre passe-bas numérique

Voir filtre numérique.

Filtre passe-bas analogique

Un filtre passe-bas peut être implémenté de façon analogique avec des composants électroniques. Ainsi, ce genre de filtre s'applique sur des signaux continus en temps réel. Les composants et la configuration du circuit fixeront les différentes caractéristiques du filtre, telles que l'ordre, la fréquence de coupure et son diagramme de Bode. Les filtres analogiques classiques sont du premier ou du second ordre. Il existe plusieurs familles de filtres analogiques : Butterworth, Tchebychev, Bessel, elliptique, etc. L'implémentation des filtres de même famille se fait généralement en utilisant la même configuration de circuit, et ceux-ci possèdent la même forme de fonction de transfert, mais ce sont les paramètres de celle-ci qui changent, donc la valeur des composants du circuit électrique.

Filtre passe-bas du premier ordre

Un filtre passe-bas du premier ordre est caractérisé par sa fréquence de coupure f_c. La fonction de transfert du filtre est obtenue en dénormalisant le filtre passe-bas normalisé en substituant ω_n par ω / ω_c, ce qui donne la fonction de transfert suivante :

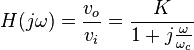
où

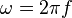
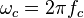
Le module et la phase de la fonction de transfert égalent à :

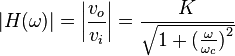
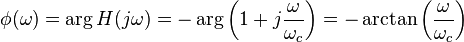
Il y a plusieurs méthodes pour implémenter ce filtre. Une réalisation active et une réalisation passive sont ici présentées. K est le gain du filtre.

Circuit passif

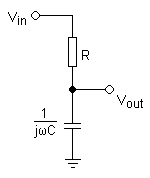
La manière la plus simple de réaliser physiquement ce filtre est d'utiliser un circuit RC. Comme son nom l'indique, ce circuit est constitué d'une résistance R et d'un condensateur de capacité C. Ces deux éléments sont placés en série avec la source v_i du signal. Le signal de sortie v_o est récupéré aux bornes du condensateur. Pour retrouver la fonction de transfert de ce filtre, il faut travailler dans le domaine de Laplace en utilisant les impédances des éléments. Avec cette technique, le circuit devient un simple diviseur de tension, et on obtient :

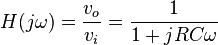
Dans cette équation, j est un nombre complexe (j tel que j²=-1) et ω est la pulsation du circuit ou fréquence radiale, exprimée en rad/s. Comme la fréquence de coupure d'un circuit RC est :

ou

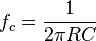
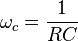
Ici ω_c, la pulsation de coupure, est également la pulsation propre ω_o du circuit, elle est également l'inverse de la constante de temps τ du circuit (majorée de la constante 2π). Ainsi, on obtient bel et bien la fonction de transfert typique du filtre passe-bas du premier ordre.

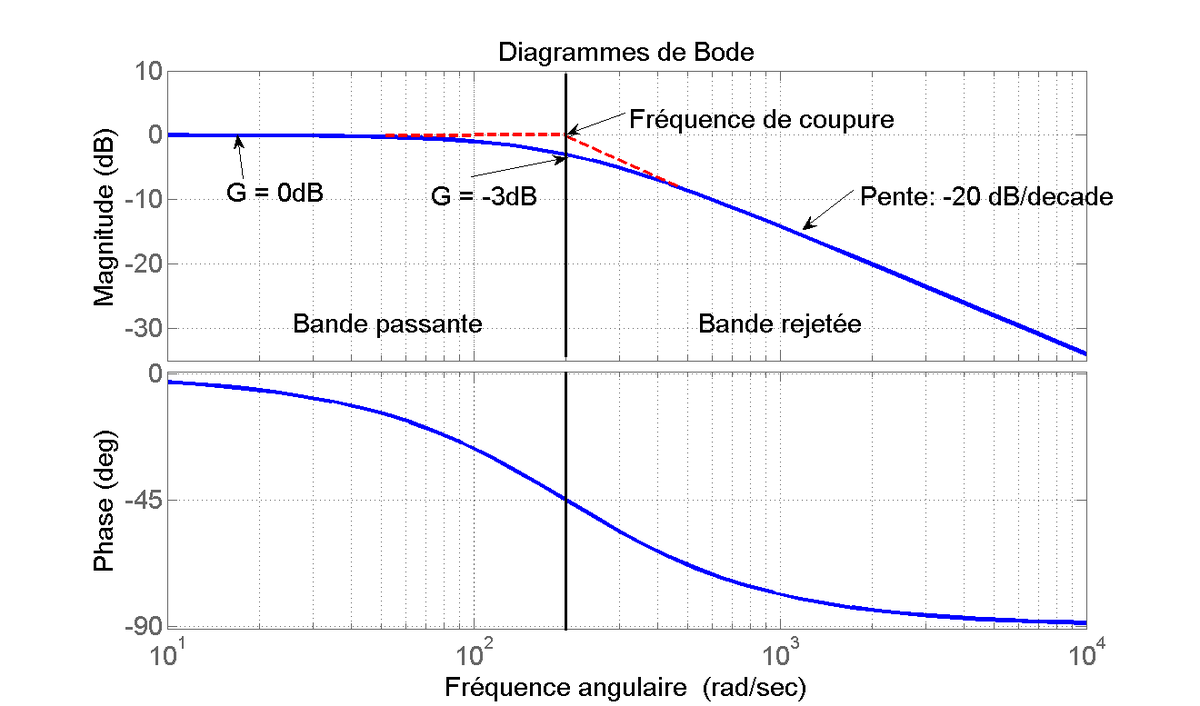
Avec cette fonction de transfert, on peut obtenir les diagrammes de Bode :

• Le gain en décibels :

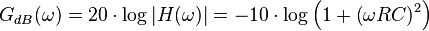
• La phase en radians :

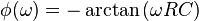
On distingue alors deux situations idéales :

• Lorsque , on a :

et (le filtre est passant)

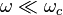
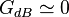
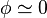
• Lorsque , on a :

et (le signal est alors filtré)

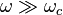
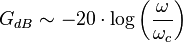
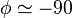
On remarque que pour ω = ω_c, on a G_dB = -3 dB.

Circuit actif

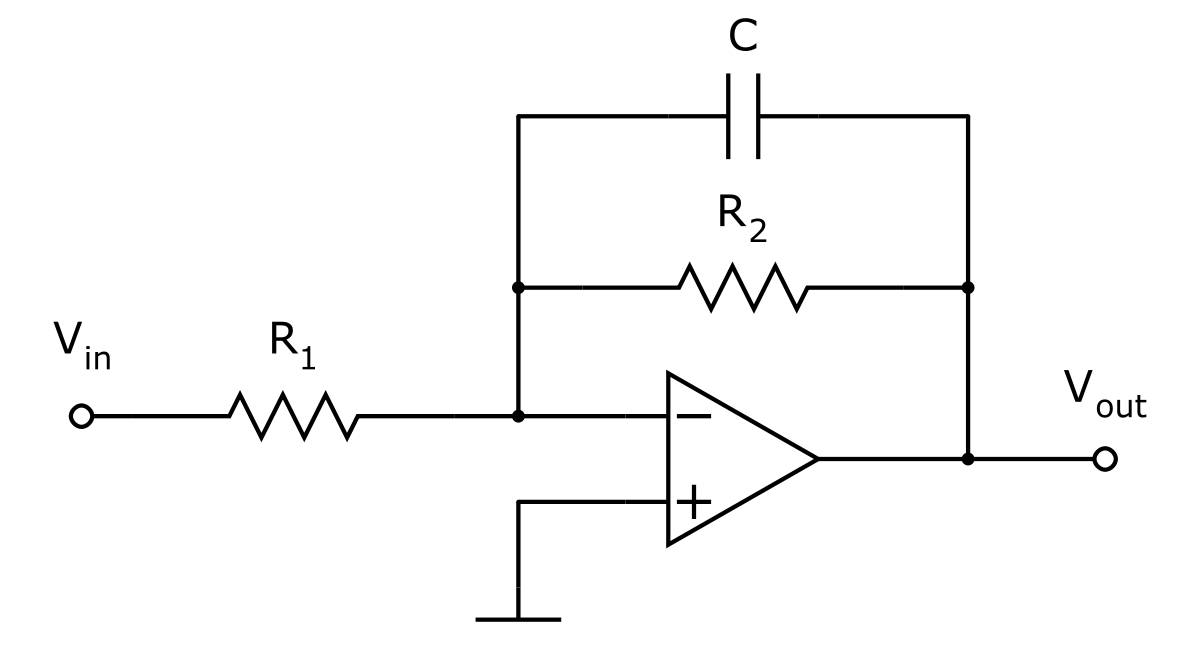
Il est également possible de réaliser un filtre passe-bas avec un circuit actif. Cette option permet d'ajouter du gain au signal de sortie, c'est-à-dire d'obtenir une amplitude supérieure à 0 dB dans la bande passante. Plusieurs configurations permettent d'implémenter ce genre de filtre.

Dans la configuration présentée ici, la fréquence de coupure se définit comme suit :

ou

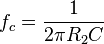
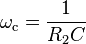
En utilisant les propriétés des amplificateurs opérationnels, et les impédances des éléments, on obtient la fonction de transfert suivante :

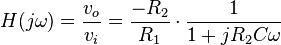
En basse fréquence, le condensateur agit comme un circuit ouvert, ce qui est confirmé par le fait que le terme de droite de l'équation précédente tend vers 1. La formule simplifiée ainsi obtenue nous donne le gain dans la bande passante :

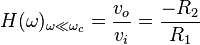
En haute fréquence, le condensateur agit comme un circuit fermé et le terme de droite tend vers 0, ce qui fait tendre la formule vers zéro.

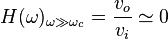
Avec la fonction de transfert, on peut démontrer que l'atténuation dans la bande rejetée est de 20 dB/décade ou de 6 dB par octave telle qu'attendu pour un filtre d'ordre 1.

Il est fréquent de voir un circuit d'amplification ou d'atténuation transformé en filtre passe-bas en ajoutant un condensateur C. Ceci diminue la réponse du circuit à haute fréquence et aide à diminuer les oscillations dans l'amplificateur. Par exemple, un amplificateur audio peut être un filtre passe-bas actif avec une fréquence de coupure de l'ordre de 100 kHz pour réduire le gain à des fréquences qui autrement oscilleraient. Cette modification du signal n'altère pas les informations « utiles » du signal, car la bande audio (bande de fréquence audible par l'humain) s'étend jusqu’à environ 20 kHz, ce qui est largement inclus dans la bande passante du circuit.

Filtre passe-bas du second ordre

Un filtre passe-bas du second ordre est caractérisé par sa fréquence de résonance f_o et par le facteur de qualité Q. Il est représenté par la fonction de transfert suivante :

où

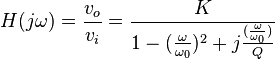
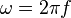
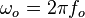
Le module et la phase de la fonction de transfert sont donc égaux à :

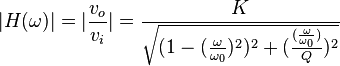
Circuit passif

La manière la plus simple de réaliser physiquement ce filtre est d'utiliser un circuit RLC. Comme son nom l'indique, ce circuit est constitué d'une résistance R, d'un condensateur de capacité C et d'une inductance L. Ces trois éléments sont placés en série avec la source v_i du signal. Le signal de sortie v_o est récupéré aux bornes du troisième et dernier élément, le condensateur. Pour retrouver la fonction de transfert de ce filtre, il faut travailler dans le domaine de Laplace en utilisant les impédances des éléments. Avec cette technique, le circuit devient un simple diviseur de tension, et on obtient :

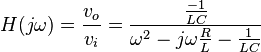
Avec :

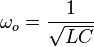
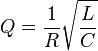
Le module et la phase de ce circuit sont :

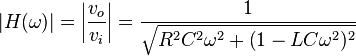
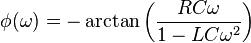
Circuit actif

Plusieurs types de filtres existent pour réaliser un filtre actif du deuxième ordre. Les plus populaires sont les structures MFB et VCVS.

Filtre d'ordre supérieur

Les filtres d'ordre supérieur sont généralement composés de filtres d'ordre 1 et 2 en cascade. La réalisation d'un filtre d'ordre 5, par exemple, se fait en plaçant deux filtres d'ordre 2 et un filtre d'ordre 1. Il serait possible de réaliser directement un filtre d'ordre 5, mais la difficulté de conception en serait grandement augmentée.