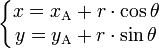Géométrie analytique - Définition
La liste des auteurs de cet article est disponible ici.
Géométrie analytique plane
Le plan affine est muni d'un repère
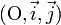
Droite
Une droite affine (c'est-à-dire une droite au sens habituel, un ensemble de points) est représentée par une équation du premier degré à deux inconnues :
- ax + by + c = 0 (1)
Si c est nul, alors la droite passe par l'origine O. Si deux droites sont parallèles, alors leurs coefficients a et b sont proportionnels. Si b n'est pas nul, cette équation peut se réécrire :
- y = a′·x + b′
a′ = - a/b est appelé le coefficient directeur ou la pente de la droite, et b′ = - c/b est appelé ordonnée à l'origine (offset ou intercept en anglais) ; deux droites parallèles ont le même coefficient directeur. Avec cette forme là, on voit aisément que la droite passe par le point (0,b′), qui est également appelé ordonnée à l'origine (le terme désigne donc à la fois le point et l'ordonnée de ce point). Si a est nul, on a une droite horizontale
- y = b′
passant par le point (0,b′). Si b est nul, on a une droite verticale
- x = - c/a
passant par le point (- c/a,0).
Pour tracer une droite à partir de son équation, il suffit de connaître deux points. Le plus simple est de prendre l'intersection avec les axes, c'est-à-dire de considérer successivement x = 0 et y = 0 (sauf si la droite est parallèle à un axe, auquel cas le tracé est trivial). On peut aussi prendre l'ordonnée à l'origine et un point « éloigné » (c'est-à-dire au bord de la figure tracée sur le papier, par exemple considérer x = 10 si l'on va jusqu'à 10), ou encore deux points éloignés (un à chaque bord de la figure) ; en effet, plus les points sont éloignés, plus le tracé de la droite est précis.
Une droite vectorielle (c'est-à-dire un ensemble de vecteurs colinéaires, proportionnels entre eux) est représentée simplement par une équation de droite avec c nul :
- au1 + bu2 = 0
où u1 et u2 sont les composantes des vecteurs. On en déduit que pour une droite affine ou vectorielle, le vecteur de composantes
est un vecteur directeur de la droite. Si le repère est orthonormé, d'après une propriété du produit scalaire, le vecteur
est un vecteur normal à la droite.
Quel que soit le repère, si A(xA,yA) est un point de la droite et

puisque
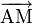

qui peut s'écrire
-
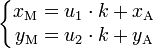
en éliminant le paramètre k, on retrouve une équation de la forme (1).
Point
Un point est représenté par un système de deux équations du premier degré à deux inconnues :
ce qui est logique puisque, un point étant l'intersection de deux droites non-parallèles, ses coordonnées doivent vérifier les équations des deux droites : la réduction de ce système d'équations donne la forme ci-dessus. Ceci est bien évidemment la représentation du point (a,b).
Demi-plan
Un demi-plan est représenté par une inéquation du premier degré à deux inconnues :
- ax + by + c > 0
si l'on remplace le signe > par un signe =, on obtient l'équation de la droite qui délimite le demi-plan ; si l'on remplace le signe > par le signe < (ou si l'on inverse les signe des coefficients), on obtient le demi-plan complémentaire.
Intersection de droites
Le plan est rapporté à un repère. Une droite (non verticale) peut être définie par une équation :
- y = ax + b.
Si on considère 2 droites définies par les équations y = ax + b et y = a'x + b', on peut savoir s'il y a une intersection ou non grâce à l'un des 3 cas suivant :
- si a = a' et b ≠ b', alors les droites sont parallèles et il n'y a pas d'intersection ;
- si a = a' et b = b', alors les 2 droites sont confondues et il y a donc une infinité de points d'intersection ;
- si a ≠ a', quels que soient b et b', il y a forcément un point d'intersection ; on obtient comme coordonnées du point d'intersection :
-
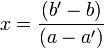
-
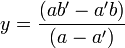
La démonstration se fait grâce à la résolution d'un système de deux équations à deux inconnues : y = ax + b et y = a'x + b'.
Demi-droite
Une demi-droite est caractérisée par une équation et une inéquation :
avec au moins a ≠a′ ou b ≠b′. Une demi-droite est en effet l'intersection d'une droite et d'un demi-plan délimité par une droite non parallèle à la première. La résolution du système obtenu en remplaçant le signe « > » par un signe « = » donne les coordonnées du point extrémité de la demi-droite, c'est-à-dire les coordonnées du point A d'une demi-droite [AB). Si a′ est non-nul, on peut se ramener à un système du type :
(les deux systèmes représentant des demi-droites complémentaires), sinon à un système du type :
Avec une équation paramétrique, cela revient à l'équation (2) en rajoutant la condition k > 0 ou k < 0.
Le cercle et le disque
Le cercle de centre A et de rayon r est l'ensemble des points situés à une distance r de A. Son équation est donc :
- (x − xA)2 + (y − yA)2 = r2
que l'on peut écrire :
Cette forme porte le nom « d'équation cartésienne du cercle ». Son équation paramétrique est :
où θ est un réel, qui peut être pris sur un intervalle de largeur 2π ; on prend en général ]-π,π] ou [0,2π[. L'équation du disque s'obtient en remplaçant le signe « égal » par un signe « inférieur ou égal ».
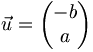
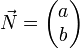
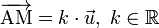
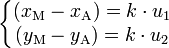
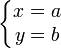



![y = y_\mathrm{A} + \sqrt{r^2 - (x-x_\mathrm{A})^2},\ x \in [x_\mathrm{A}-r,x_\mathrm{A}+r]](https://static.techno-science.net/illustration/Definitions/autres/6/6b7638085e6d29ec5ed65a5cab240abc_b27bc2deba751982a577a3a3c9abd22c.png)