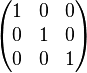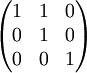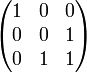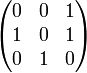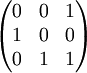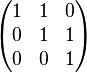Groupe simple d'ordre 168 - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en théorie des groupes, un groupe simple est un groupe qui n'admet aucun sous-groupe distingué propre. La classification des groupes simples finis montre qu'il est possible de les ranger en quatre catégories : les groupes cycliques d'ordre un nombre premier, les groupes alternés, les groupes de type Lie et les groupes sporadiques.
Le plus petit groupe simple de type Lie est d'ordre 168 ; il est le premier élément de sa catégorie. C'est, à isomorphisme près, le seul groupe simple d'ordre 168. Il peut être vu comme le groupe linéaire d'un espace vectoriel de dimension 3 sur le corps F2, ou encore comme le groupe spécial linéaire (des automorphismes de déterminant égal à 1) d'un espace de dimension 2 sur le corps F7. Il peut aussi être vu comme le groupe de Galois d'une équation du septième degré, ou le groupe des automorphismes laissant invariant la quartique de Klein la courbe du plan projectif complexe définie par le polynôme P suivant :
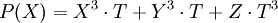
Ce groupe intervient par exemple dans une démonstration du dernier théorème de Fermat pour le paramètre n égal à 7.
Groupe linéaire GL3(F2)
Classe de conjugaison
Etudions le groupe linéaire d'un espace vectoriel E de dimension 3 sur le corps fini F2 à deux éléments. Ce groupe est noté G.
Si φ est un élément de G et (e1, e2, e3) une base de E, φ(e1) peut prendre 7 valeurs distinctes, toutes celles différentes du vecteur nul. Le vecteur φ(e2) peut être choisi dans un ensemble de 6 valeurs, à savoir tous les vecteurs non colinéaires à φ(e1). Enfin, φ(e3) est un vecteur quelconque hors du plan engendré par φ(e1) et φ(e2), soit 4 valeurs possibles, ce qui établit la proposition suivante :
-
- Le groupe GL3(F2) est d'ordre 168.
Le tableau des classes de conjugaison du groupe est le suivant :
|
La première colonne du tableau indique une matrice d'un représentant quelconque de la classe dans une base bien choisie. La deuxième colonne est le polynôme minimal d'un représentant, la troisième colonne est l'ordre d'un élément et la quatrième indique l'ordre de son centralisateur, c'est-à-dire le groupe des éléments qui commutent avec le représentant.
Une technique simple pour déterminer les classes de conjugaison est l'étude des différents polynômes minimaux. Aucun d'entre eux ne peut avoir une constante nulle, car l'endomorphisme associé n'est pas injectif.
Il existe un unique polynôme minimal possible du premier degré, X + 1, qui correspond à l'endomorphisme identité.
Le polynôme minimal X2 + 1 est égal à (X + 1)2. L'endomorphisme associé est la somme de l'identité et d'un endomorphisme nilpotent N d'ordre 2, la matrice s'obtient par une réduction de Jordan. Le calcul du centralisateur s'obtient par la détermination des automorphismes qui commutent avec N. Si l'on choisit une base (e1, e2, e3) tel que N(e1) et N(e2) soit le vecteur nul et N( e3) soit égal à e1, la matrice d'un automorphisme commutant avec N est de la forme :

On trouve 8 automorphismes. Comme l'ordre du centralisateur d'un représentant d'une classe de conjugaison que multiplie le cardinal de la classe est égal à l'ordre du groupe (cf Action par conjugaison), le cardinal de la classe est égal à 21.
X2 + X + 1, correspond au polynôme minimal un endomorphisme diagonalisable dans F4, l'extension de F2 de degré 2. Dans ce corps, l'endomorphisme possède trois valeurs propres dont l'une correspond à un espace vectoriel de dimension 2. La trace d'un tel automorphisme n'est pas dans F2, ce polynôme minimal n'est jamais obtenu pour un automorphisme de E.
Le polynôme minimal X3 + 1 se factorise en (X + 1)(X2 + X + 1). L'automorphisme associé possède 1 pour valeur propre et l'espace propre associé est de dimension 1 et il existe un espace stable de dimension 2 tel que X2 + X + 1 est le polynôme minimal de la restriction de l'automorphisme à cet espace de dimension 2. Si e1 est le vecteur propre de valeur propre 1, si e2 est un vecteur non nul de l'espace stable de dimension 2 et si e3 est l'image de e2 par l'automorphisme, on trouve bien la matrice indiquée. Un automorphisme commutant avec cet élément s'écrit, dans une telle base :
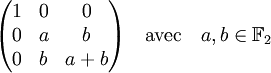
On remarque que a et b ne peuvent être simultanément nuls, ce qui fait un centralisateur à 3 éléments.
Les polynômes minimaux X3 + X + 1 et X3 + X2 + 1 se traitent de la même manière. On remarque que :
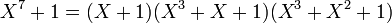
On en déduit que les deux classes de conjugaison contiennent des éléments d'ordre 7. Le centralisateur d'un représentant φ contient au moins 7 éléments, les puissances de φ. Il est de plus dans l'espace vectoriel de cardinal 8 engendré par I, φ et φ2. Le centralisateur contient donc exactement 7 éléments.
Enfin, le polynôme minimal X3 + X2 + X + 1 vérifie l'égalité X4 + 1=(X + 1)(X3 + X2 + X + 1), un automorphisme associé est d'ordre 4. Une décomposition de Jordan donne la forme matricielle proposée et montre que l'automorphisme est la somme de l'identité et d'un endomorphisme nilpotent d'ordre 3 car le polynôme minimal s'écrit aussi (X + 1)3. Un automorphisme commutant avec un élément de cette classe s'écrit I + a.N + b.N2, ce qui montre que le centralisateur est d'ordre 4.
Caractère
La détermination des classes de conjugaison permet d'établir la table des caractères du groupe. Comme il existe 6 classes de conjugaison, il existe exactement 6 représentations irréductibles, à un isomorphisme près dans des espaces vectoriels complexes. Les classes sont nommées en fonction de l'ordre de leurs éléments et les représentations en fonction de leur dimension. Comme il existe 2 représentations de dimension 3 et deux classes composées d'éléments d'ordre 7, ces classes et ces représentations sont indexées par une lettre. On obtient la table suivante :
|
-
- Représentation de dimension 1 :
Remarquons, dans un premier temps qu'il n'existe pas de morphisme surjectif du groupe dans un groupe cyclique de plus d'un élément. En effet, pour que le morphisme soit surjectif, le groupe d'arrivée possède nécessairement un ordre qui divise 168. Si un tel morphisme existait, il existerait nécessairement un morphisme surjectif dans un groupe cyclique d'ordre 2, 3 ou 7. Un morphisme à valeur dans un groupe cyclique d'ordre 2 est nul sur les classes C3, C7a et C7b, c'est-à-dire sur plus de la moitié des éléments du groupe G, un tel morphisme a nécessairement pour image l'élément neutre. Un morphisme dans un groupe cyclique d'ordre 3 est nécessairement nul sur les classes C4, C7a et C7b, il est donc nul. Le même raisonnement montre qu'il est aussi nul s'il est à valeur dans un groupe d'ordre 7. Comme tout caractère de dimension 1 est aussi un morphisme d'image un groupe cyclique, le seul caractère de dimension 1 est le caractère trivial.
-
- Représentation de dimension 2 :
Il n'existe pas de représentation irréductible de dimension 2. Pour cela, il suffit de considérer la trace de l'image φ d'un élément de C7a. L'automorphisme φ est diagonalisable car son polynôme minimal est un diviseur de X7 - 1 et il ne possède pas de racine multiple. On en déduit qu'il admet deux valeurs propres λ et μ, toutes deux racines septièmes de l'unité. On remarque que φ2 est aussi dans C7a ce qui montre que λ + μ est égal à λ2 + μ2. Cet égalité fournit un polynôme de degré inférieur ou égal à 6, différent du polynôme cyclotomique d'indice 7 et ayant une racine septième de l'unité. On en déduit que λ et μ sont tous les deux égaux à 1. La trace de l'image d'un élément C7a ou de C7b est nécessairement égale à 2. Le calcul de la norme du caractère associé à cette représentation donne un résultat strictement supérieur à 1, ce qui montre que la représentation n'est pas irréductible.
-
- Dimensions des différentes représentations irréductibles :
Il existe une unique représentation de dimension 1 et aucune de dimension 2. De plus, si di décrit toutes les dimensions des représentations irréductibles, on dispose de l'égalité suivante (cf Représentation régulière) :
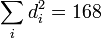
Il n'existe qu'une unique manière de décomposer 168 en somme de carrés parfaits tous différents de 4 et avec un unique carré égal à 1. Les dimensions des représentations irréductibles sont donc 1, 3, 3, 6, 7 et 8. Ceci permet de remplir la première ligne et la première colonne du tableau.
-
- Représentations de dimension 3 :
Déterminons les caractères des représentations irréductibles de dimension 3. Le même raisonnement que précédemment montre que si φ est un automorphisme image d'un élément de C7a, il possède comme valeurs propres trois racines primitives septième de l'unité λ, λa et λb, où a et b sont deux entiers compris entre 1 et 6 tel que a est plus petit que b. Comme la trace de φ est égale à celle de φ2 la valeur λ + λa + λb est égale à la valeur λ2 + λ2a + λ2b est a est égal à 2 et b à 4. On remarque que la somme de λ + λ2 + λ4 et de λ3 + λ5 + λ6 est égale à -1 et le produit à 2. On en déduit que le caractère sur la classe C7a est égal à 1/2.(-1 ± i√7). Le produit scalaire de χ1 et de χ3a est égal à 0. De plus, l'expression i√7 ne se retrouve dans le caractère d'aucune classe autre que C7a et C7b, on en déduit que si le caractère est égal à 1/2.(-1 + i√7) sur C7a, il vaut nécessairement 1/2.(-1 - i√7)C7b et vis-versa.
Un raisonnement analogue montre que les valeurs propres d'un automorphisme image d'un élément de C3 possède trois valeurs propres distinctes et toutes trois racines troisièmes de l'unité, ce qui montre que le caractère est nul sur cette classe, car la somme des trois racines est nulle.
Pour les automorphismes image d'un élément de C2, les valeurs propres sont, soit 1 soit -1 et la trace est égale à 1 ou 3 en valeur absolue. Comme la norme du caractère est égale à 1, 3 en valeur absolue n'est pas une valeur possible. Pour C4, un raisonnement analogue montre que la trace est égale à 1 en valeur absolue. L'orthogonalité de χ3a avec χ1 permet de déterminer les signes manquants. Le raisonnement s'applique de la même manière à χ3b.
-
- Autres représentations :
Le raisonnement précédent montre que la trace d'un automorphisme image d'un élément de C7a est l'une des trois valeurs : -1, -1 + i√7 ou -1 - i√7, si la dimension de la représentation irréductible est égale à 6. Les deux dernières valeurs sont impossibles car la norme du caractère serait strictement supérieure à 1. Le calcul des produits scalaires de χ6 avec χ1, χ3a et χ6 permet de conclure.
Pour la représentation de dimension 7, les six coefficients restant à déterminer se calculent avec les produits scalaires entre le caractère à déterminer et les précédents. Il n'existe qu'une seule solution de norme 1. Enfin, la connaissance du caractère de la représentation régulière et des 5 premiers caractères permet le calcul de χ8.
Simplicité
-
- Le groupe GL3(F2) est simple.
Une manière simple de s'en rendre compte est d'étudier la table des caractères. À l'exception du caractère trivial, ils sont tous associés à des représentations fidèles, c'est-à-dire injectives. Pour le vérifier il suffit de remarquer que la trace de l'identité n'est obtenue que pour l'image de l'élément neutre. Si le groupe possédait un sous-groupe distingué non trivial, il existerait un morphisme de G non injectif et non trivial. Le morphisme et une représentation du groupe d'arrivée fournirait une représentation non injective et non triviale.
Il existe aussi une démonstration directe
Soit H un sous-groupe distingué non trivial de G. Si H ne contient ni élément d'ordre 7, ni élément d'ordre 3. Son ordre est un diviseur de 168 que divise 12, c'est-à-dire 8. Or H contient nécessairement un élément d'ordre 2, il contient alors au moins les 21 éléments d'ordre 2, ce qui est impossible.
Si H contient un élément d'ordre 3, il les contient alors tous car ils sont dans la même classe de conjugaison. En ajoutant l'élément neutre, on trouve au moins 57 éléments dans le groupe. Le seul diviseur de 168 plus grand que 57 est 84, ce qui montre que H contient un élément d'ordre 2 et un élément d'ordre 7, ce qui montre que la classe des éléments d'ordre 2 et une classe d'éléments d'ordre 7 est dans le groupe H. L'ordre de H est strictement supérieur à 84, le seul diviseur supérieur à 84 de 168 est 168, H est donc le groupe G.
Si H contient un élément d'ordre 7, H contient au moins 25 éléments. Les entiers supérieurs à 25 divisant 168 sont 168, 84, 56, 42 et 28. Tous ces diviseurs sont des multiples de 2, ce qui montre que H contient la classe des éléments d'ordre 2, c'est-à-dire au moins 46 éléments. Il ne reste plus que 3 ordres candidats, 168, 84 et 56. Le 2-groupe maximal est d'ordre 8, un théorème de Sylow indique que tous les 2-groupes maximaux de G contiennent sont isomorphes et contiennent un élément d'ordre 4. Un groupe d'ordre 56 contient nécessairement un tel groupe et donc un élément d'ordre 4, ce qui montre que la classe des éléments d'ordre 4 est dans H, H contient au moins 88 éléments donc G tout entier. Il ne reste plus que le cardinal 84, contenant nécessairement un élément d'ordre 3 et donc le groupe entier.