Harmonice Mundi - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Les origines - Dès la Renaissance - La musique des sphères de l'Antiquité au Moyen Âge - La notion d'harmonie

La notion d'harmonie

L'harmonie part d'une constatation simple, musicale. Lorsque deux sons harmonieux sont combinés, ils se mélangent et le son devient plus fort (notion de consonance qui aboutira au concept d'accord). Lorsque 2 sons non harmonieux sont combinés, ils ont tendance à s'annihiler (notion de dissonance).

De plus, il est constaté qu'en appuyant sur une corde vibrante à sa moitié, on obtient une note fortement consonance d'avec la corde vibrant à vide (en fait, la fréquence double de celle-ci, l'octave). De même, si l'on bloque la même corde au tiers, ou bien aux deux tiers de sa longueur, on obtiendra également une note fortement consonante (en fait la fréquence triple de la fondamentale, la quinte).

L'analyse de Fourrier a expliqué les raisons des harmoniques. L'équation des cordes vibrantes les modélise bien. En fonction des contraintes extérieures, une corde s'auto-ajuste (de même qu'une membrane). Quelle que soit la tension qu'on applique à ses extrémités, bloquer la corde à sa moitié, ou à son tiers, provoquera toujours une octave (fréquence double) ou une quinte (fréquence triple) par rapport à la même corde vibrant à vide (fréquence fondamentale). Kepler a généralisé cette approche à l'espace cosmique : les orbites des planètes s'auto-ajustent, dans des rapports entiers. D'où son essai, l'harmonie du monde.

Du point de vue des gammes musicales, le défit était de fonder une gamme qui permettaient de parcourir toutes les notes consonantes en partant d'un point. Il n'y avait pas de résolution exacte à ce problème, mais il en existe une résolution approchée, la gamme (bien) tempérée.

En effet, il n'est pas possible de fonder une gamme contenant toutes la suite des quintes et l'octave en même temps, en partant d'une note fondamentale.

La suite des octaves, la suite des fréquences doubles, s'écrit mathématiquement $f = f 0 .2 i$ ( $f 0$ , fréquence fondamentale)
La suite des quintes, la suite des fréquences triple, s'écrit mathématiquement $f = f 0 .3 j$ ( $f 0$ , fréquence fondamentale)

Or trouver i, j tels que $2 i = 3 j$ , n'a pas de solution pour i et j entiers, et il est nécessaire d'avoir un nombre entier de notes dans une gamme.

La solution approchée à ce problème :

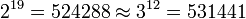
$2^{19} = 524288 \approx 3^{12} = 531441$

Autrement dit, la 19ème octave d'une note fondamentale est proche de sa 12ème quinte. En répartissant cet écart sur douze note (diminuant légèrement chacune des quintes pour arriver à l'octave) et ramenant chacune de ces notes sur un seul octave, Jean-Sébastien Bach a créé la gamme tempérée, où tous les demis-tons sont égaux.

C'est-à-dire que la valeur du demi-ton de la gamme tempérée est (multiplicateur de la fréquence de la note précédente s'entend) :

$dt = \sqrt[12]{\left(3^{12}-\left(3^{12}-2^{19}\right)\right)/2^{18}} = \sqrt[12]{2} \approx 1,05946309$ .

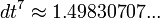
D'où la quinte approchée $dt^{7} \approx 1.49830707...$

Cela est légèrement inférieur à la quinte juste, mais cela reste acceptable. L'octave est en revanche parfaitement juste. Cette approche fut permise par l'invention des logarithme par John Napier (dit Neper), lesquels furent abondamment utilisés en astronomie, en particulier par Kepler, même si celui-ci réfléchissait en termes de rapports entiers, selon les règles harmoniques.

Pythagore avait défini sa gamme différemment. En partant d'une note de base, par exemple le " do ", il multiplia sa fréquence par 3/2 afin de définir sa quinte supérieure " sol " et répéta cette opération pour construire des suites de quintes " ré - la - mi - si ". Il réalisa ce calcul après avoir observé que la longueur d'une corde donnant la quinte d'un son était égale aux 2/3 de celle fournissant son fondamental. Procéder ainsi, c'est " ignorer " les octaves qui sont alors trop grandes d'une valeur d'un neuvième de ton (le commas Pythagoricien). Mais, comme les lyres n'avaient pas plus de 7 cordes, cela n'avait pas d'importance ! De plus, sur le plan philosophique, l'idée d'infinité de la gamme en spirale est assez satisfaisante. C'est plus gênant maintenant pour un piano où apparaît une différence d'un demi-ton au bout de 4 octaves.

D'autres approches consistaient en demi-tons de valeur variable (diatonique, chromatique)

Citation

« C'est l'expérience infaillible de l'harmonie entre les évènements terrestres et les changements célestes qui a instruit et forgé malgré moi ma conviction » Johannes Kepler