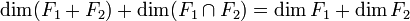Hermann Günther Grassmann - Définition
La liste des auteurs de cet article est disponible ici.
Travaux en linguistique
La loi de Grassmann, est la « loi de dissimilation des aspirées », c'est une loi de phonétique qui décrit les modifications survenus dans une phase préhistorique des langues indo-européennes, tant en grec ancien qu'en sanskrit. Ces modifications se poursuivent tout au long de leur histoire. Communes aux deux langues, elles sont connues et expliquées par les grammairiens indiens, mais porte le nom de leur « découvreur » occidental. Elle porte sur les successions de voyelles aspirées, dont la première devient dissimulée. On retrouve cette loi tant au stade préhistorique, qu'au stade historique. Elle possède des peudo-formes irrégulières et l'explication de son origine est encore controversée.
L'inventeur des structures vectorielles
L’étude de la géométrie dans un cadre général, où s'abolissent les particularités des dimensions 2 et 3 est l’idée forte de Grassmann. La notion de vecteurs, apparu pour la première fois chez Simon Stevin à la fin du XVIe siècle, avait déjà pleinement évoluée. Imitant François Viète, le philosophe Leibniz (1646-1716) développe en 1679 (dans une lettre à Huygens) l'exposé de premiers calculs sur les entités géométriques. Toutefois, cette intuition demandait à être formalisée dans le cadre d'une théorie qui la dépouille des points, et en donne une axiomatique rigoureuse.
En 1835, l'italien Bellavitis (1803-1880), professeur à l'université de Padoue, publie un premier ouvrage sur le calcul des lignes équipollentes (nos vecteurs actuels).
En 1839, dans sa thèse « Théorie des flots et des marées », Grassmann utilise ces méthodes vectorielles. Mais cette thèse n'est même pas lue par son examinateur. Et elle ne sera publiée qu'en 1911. C'est pourtant dans cette thèse, que Grassmann définit la somme de deux vecteurs dans l'espace, leur déterminant (comme l'aire de la surface orientée du parallélogramme qu'ils engendrent), le déterminant de trois vecteurs de l'espace (comme volume du parallélépipède orienté qu'ils engendrent)....
Ce calcul vectoriel apparaît comme l'ancêtre du notre et permet à Grassmann de simplifier les calculs que Lagrange avait fait dans la « Mécanique analytique ».
Par la suite, le travail d'axiomatisation se poursuit XIXe siècle sous l'impulsion d'Hamilton et de Grassmann.
En 1843, Hamilton donne une première version de ses quaternions (en dimension 4 donc).
En 1844, dans son Ausdehnungslehre, Grassmann développe l'idée d'une structure algébrique dans laquelle les symboles représentant des quantités (points, droites, plans) sont régis par des règles ; ce faisant, il dégage une structure géométrico-algébrique générale, proche de la conception axiomatisée actuelle des espaces vectoriels de dimension finie.
Ces idées sont plus riches et plus générales que celles exposées par Hamilton ; ici l'algèbre linéaire prend véritablement naissance et cet ouvrage Die Lineare Ausdehnungslehre, ein neuer Zweig der Mathematik [L'enseignement de l'extension linéaire, une nouvelle branche des mathématiques], semble la première publication importante dans le cadre de la théorie des espaces vectoriels. Néanmoins, réalisée « en marge des milieux académiques », cette théorie et les méthodes de calculs de Grassmann, que l'on regroupe aujourd'hui sous le terme de calcul vectoriel, passent pratiquement inaperçue.
Il y définit pourtant le produit scalaire et le produit extérieur, généralisation de ce que Willard Gibbs et William Kingdon Clifford appellent en dimension 3, le produit vectoriel. Il y dénonce aussi le piège de la confusion entre nombre et grandeur. Malheureusement, bien trop en avance sur son temps, abstrait et assez mal écrit ce livre demeure, de fait, ignoré pendant quinze ans.
Il faut attendre 1860, pour que les mathématiciens italiens Cremona, Bellavitis, et Peano commencent à s'y intéresser. En 1862, la réimpression de l'Ausdehnungslehre, débarrassée de ses considérations philosophiques, et augmentée de résolutions de problèmes nouveaux (solution du problème de Pfaff) est plus complète et plus lisible.
Ce sont alors les compatriotes de Grassmann, Hankel (1867), Victor Schlegel (1869), Clebsch (1872) et Klein qui lui marquent leur sympathie. Schlegel diffuse l'œuvre de Grassmann au travers de ses élèves. Mais la véritable reconnaissance lui viendra de l'américain Gibbs qui, avec Klein, rassemble ses œuvres et les publie entre 1894 et 1911. A cette époque les héritiers d'Hamilton, dont Tait, s'opposent aux développement du calcul vectoriel, au nom d'une fidélité aux quaternions.
Après eux viendront Maxwell et Clifford (1845-1879), qui fut l'un des premiers mathématiciens à célébrer ensemble Grassmann et Hamilton. celui-ci publie en 1878] une « Application de l'algèbre de l'extension de Grassmann ».
En l'honneur de Grassmann, on a baptisé Grassmanniennes les variétés (de l’espace projectif) formées par les sous espaces de dimension k d’un espace vectoriel de dimension n. Celles-ci formaient le but de ses recherches ; il s'agit d'un ensemble, muni de sa topologie, dont les éléments sont les sous-espaces vectoriels de même dimension d'un espace vectoriel fixé. On note G(k,n) la grassmanienne des sous-espaces de dimension k dans un espace de dimension n. La métrique en est donnée par {d(E,F) = inf | | | I − g | | | ,g(E) = F} où g parcourt l'ensemble des isométries affines. qui en fait un espace métrique.
On lui doit également le théorème des dimensions, qu'on appelle aujourd'hui formule de Grassmann :
E étant un espace vectoriel de dimension finie, si F1 et F2 sont deux sous-espaces vectoriels de E, alors