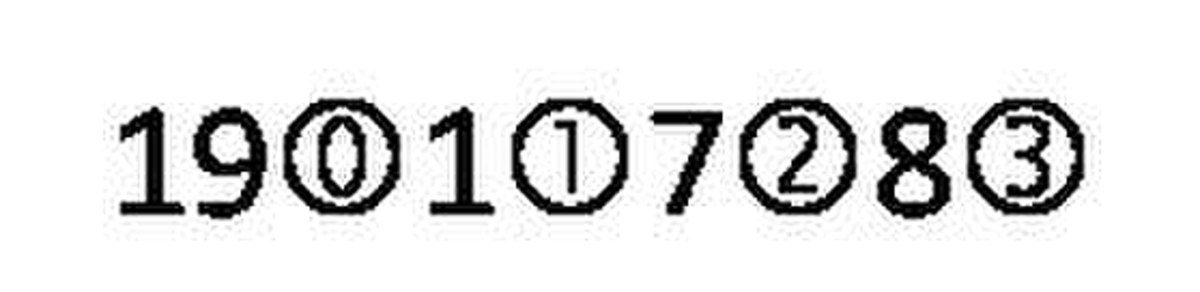Simon Stevin - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Simon Stevin (1548 à Bruges - 1620) fut un ingénieur, un mécanicien et un mathématicien flamand (Belgique).
« Wonder en is gheen wonder » fut sa devise.
Éléments biographiques
Commis d’un marchand à Anvers de 1564 aux années 1570, Stevin fut employé aux finances du port de Bruges en 1577. Il ne parvint pas à obtenir la franchise des droits sur la bière, et s'expatria l'année suivante : il travailla en Prusse, en Pologne, au Danemark, en Suède et en Norvège. De retour aux Pays Bas en 1581, à 33 ans, il publia un livre sur le calcul des intérêts puis s'inscrivit à l'université de Leyde en 1583.
C'est sans doute à l'université que Stevin découvre l'œuvre d'Archimède dans la traduction de Maurolico intitulée les Monumenta (Palerme). Stevin fait dès lors ses premières recherches sur les machines qu'il a vu fonctionner dans les différents arsenaux de la mer du Nord et la fin des années 1580 voit la parution, chez l'imprimeur huguenot Christophe Plantin, de ses principaux ouvrages, notamment la Statique ou l'Art de peser (1586) et l'hydrostatique (1586).
Ces travaux lui attirent la faveur du prince Maurice de Nassau, qui le consultera désormais souvent et en fera le premier intendant des canaux de la République des Provinces Unies. En 1590, Stevin déménage à Delft puis à La Haye. Devant l'ampleur des travaux à mener pour défendre les villes de la jeune république, il plaide pour un enseignement universitaire sur l'Artillerie et les Fortifications . En 1593, Il fait partie des mathématiciens du monde entier pressentis par Adrien Romain pour résoudre son équation de degré 45, et dont François Viète triomphera. En 1600, il fonde à Leyde avec l'appui de Maurice de Nassau une école d'ingénieurs militaires annexée à l'université (mais indépendante de celle-ci) : Jacques Aleaume l'y assiste dès 1607, étant formé à l'algèbre dans l'esprit de Viète. Descartes, Guez de Balzac et bien d'autres jeunes aristocrates français viendront y rechercher la formation scientifique et technique qui fait défaut dans leur pays, dévasté par les Guerres de Religion et en proie à l'instabilité politique.
On connaît peu de choses sur de la vie privée de Stevin ; il a laissé une veuve et deux enfants. À Bruges, une place porte son nom et on peut y voir une statue réalisée par Eugen Simonis. Il a également laissé son nom à la rue Stévin, située dans l'un des quartiers les plus prisés de Bruxelles, à deux pas du rond-point Schuman et du square Ambiorix.
Philosophie des sciences
Stevin était convaincu qu'un âge de raison avait existé dans le passé (Hugo Grotius). Patriote, il s'efforça de faire des dialectes bas-allemands parlés dans les Pays Bas une langue à part entière, et s'évertua notamment à trouver un équivalent flamand/néerlandais, pour tous les termes scientifiques et techniques : ainsi le mot hollandais pour mathématiques n'a pas de racine grecque mais germanique : Wiskunde. Stevin voyait l'avantage du néerlandais dans le nombre de mots monosyllabiques et la faculté de composer des radicaux.
Mathématiques
La comptabilité en partie double peut avoir été connue par Stevin soit lorsqu'il était clerc à Anvers, soit à travers les œuvres des auteurs italiens comme Luca Pacioli et Girolamo Cardano. Cependant, il fut le premier à recommander l’utilisation de comptes impersonnels dans la comptabilité nationale. Il le pratiqua pour le prince Maurice et le recommanda à Sully.
Son plus grand succès fut un petit traité appelé De Thiende (La dîme), publié comme tous ses écrits en hollandais en 1586 et ne dépassant pas sept pages dans la traduction en français.
Les fractions décimales avaient été employées pour l’extraction des racines carrées quelques cinq siècles avant son époque mais personne avant Stevin n'avait montré l'intérêt de son emploi quotidien.
Stevin fut si conscient de l’importance de cette contribution qu’il déclara que l’utilisation universelle du système décimal était inéluctable. La notation qu'il propose est plutôt difficile à manier : les décimales sont affectées de leur puissance de dix, marquées par un petit cercle autour de l'exposant.
Stevin note d'ailleurs ainsi dans les équations algébriques les nombres élevés à une puissance : des nombres encerclés dénotent de simples exposants. Stevin utilise les exposants fractionnels, mais ne considère jamais d'exposants négatifs.
La notation décimale de Stevin trouva un écho dans l'Europe savante. La virgule décimale fut introduite par Bartholomäus Pitiscus dans ses tables trigonométriques (1612), et fut reprise par John Napier dans ses deux ouvrages sur les tables de logarithmes (1614 et 1619).
Stevin innova finalement peu en géométrie, mais fut le premier à montrer comment construire un polyèdre en le développant sur un plan.
Mécanique
L'apport de Stevin à la Statique (1586) est considérable. Montrant que tout équilibre peut se ramener en dernière analyse à une forme abstraite de pesée, il donne à entendre que derrière la notion de poids se cache une notion abstraite, plus générale, celle de force. Par cette méthode, il approche de la notion de moment d'une force en généralisant le principe du levier avec une plus grande hardiesse que tous ses prédécesseurs (Cardan, Tartaglia). Il réduit ainsi la loi de l’équilibre sur un plan incliné à celle d'un équilibre de levier. Célèbre est l'analyse de Pierre Duhem de l'épistémologie de ses réflexions (pour Archimède, contre Aristote). Il utilise aussi la notion de déplacement virtuel, qui sera reprise par Galilée. Il dégage enfin le premier les notions d'équilibre stable et instable .
Il démontra, un siècle avant Pierre Varignon la méthode du parallélogramme des forces, laquelle n'était connue auparavant que dans des cas particuliers (poussées égales en intensité et concourant à angle droit, ou à 60°). L'anecdote citée précédemment du char à voile montre qu'il a compris comment remonter au vent, ce qui dénote une large avance sur son époque.
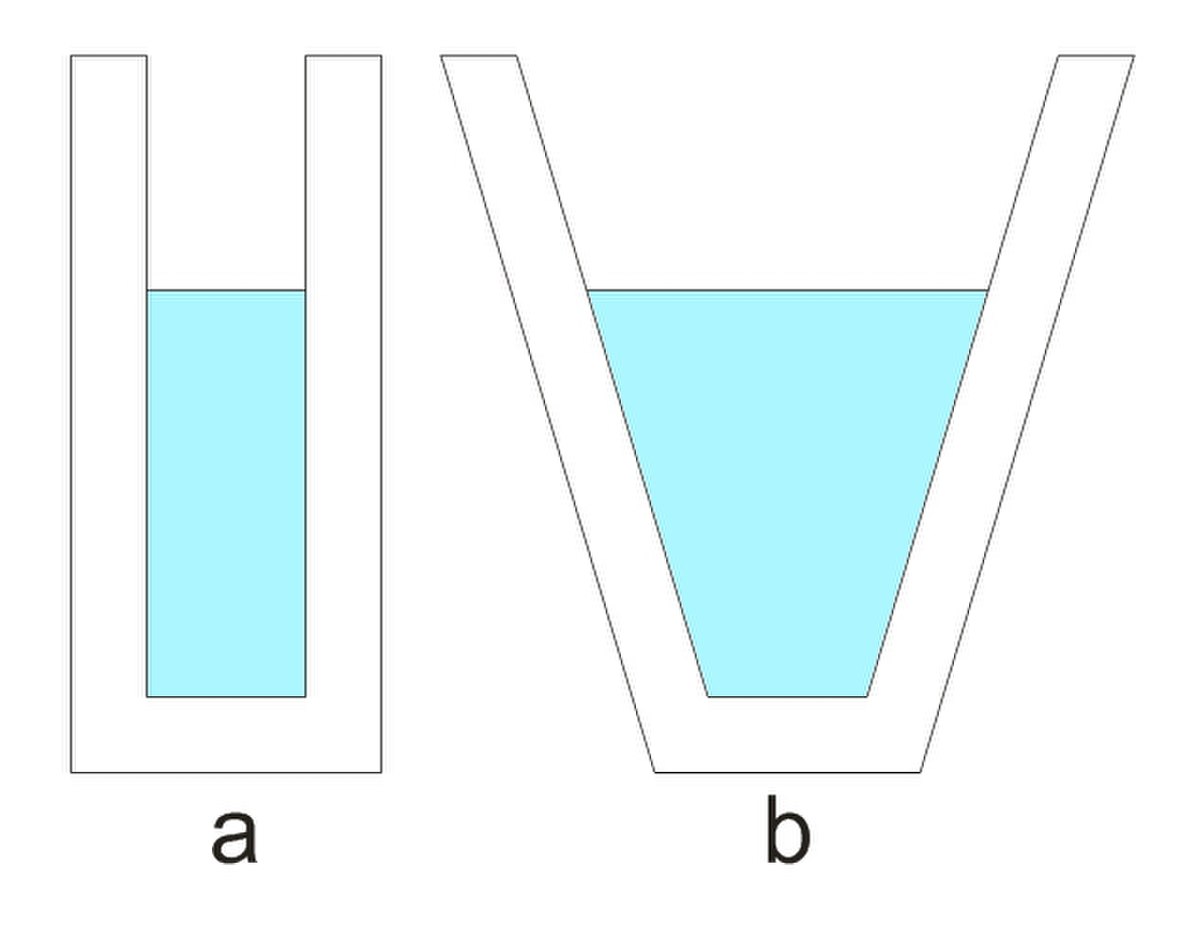
Il découvrit le paradoxe hydrostatique : la pression d’un liquide sur le fond d'un récipient est indépendante de sa forme, et aussi de la surface du fond ; elle dépend seulement de la hauteur d'eau dans le récipient. Il donna aussi la mesure de la pression sur n'importe quelle portion du côté d’un récipient.
En 1606, il démontra que deux objets de poids différents tombent avec la même vitesse.
Il tenta enfin d'expliquer les marées par l’attraction de la lune.
Il précède donc Galilée sur de nombreux points ; mais son œuvre immense reste largement méconnue : le courant flamand ne sera traduit que plus tard, et l'on connaîtra surtout la pensée italienne ( Benedetti, etc.), issue de Leonardo, Cardan, Tartaglia.