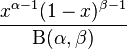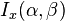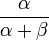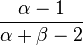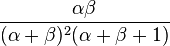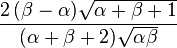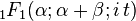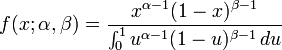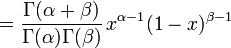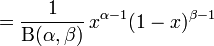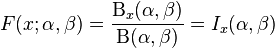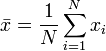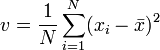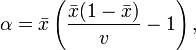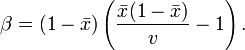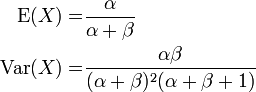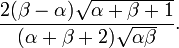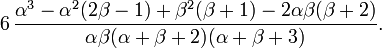Loi bêta - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Beta | |
|---|---|
| |
| |
| | |
| Paramètres | α > 0 forme (réel) β > 0 forme (réel) |
| Support |
|
| Densité de probabilité (fonction de masse) |
|
| Fonction de répartition |
|
| Espérance |
|
| Mode |
|
| Variance |
|
| Asymétrie (statistique) |
|
| Kurtosis (non-normalisé) | see text |
| Entropie | see text |
| Fonction génératrice des moments |
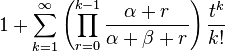
|
| Fonction caractéristique |
|
| modifier | |
Dans la théorie des probabilités et en statistiques, la loi bêta est une famille de lois de probabilités continues, définies sur [0,1], paramétrisée par deux paramètres de forme, typiquement notés α et β. C'est un cas spécial de la distribution de Dirichlet, avec seulement deux paramètres.
Caractérisation
Fonction de densité
La densité de probabilité de la loi bêta est:
où Γ est la fonction gamma. La fonction bêta, B, apparaît comme une constante de normalisation, permettant à la densité de s'intégrer à l'unité.
Fonction de répartition
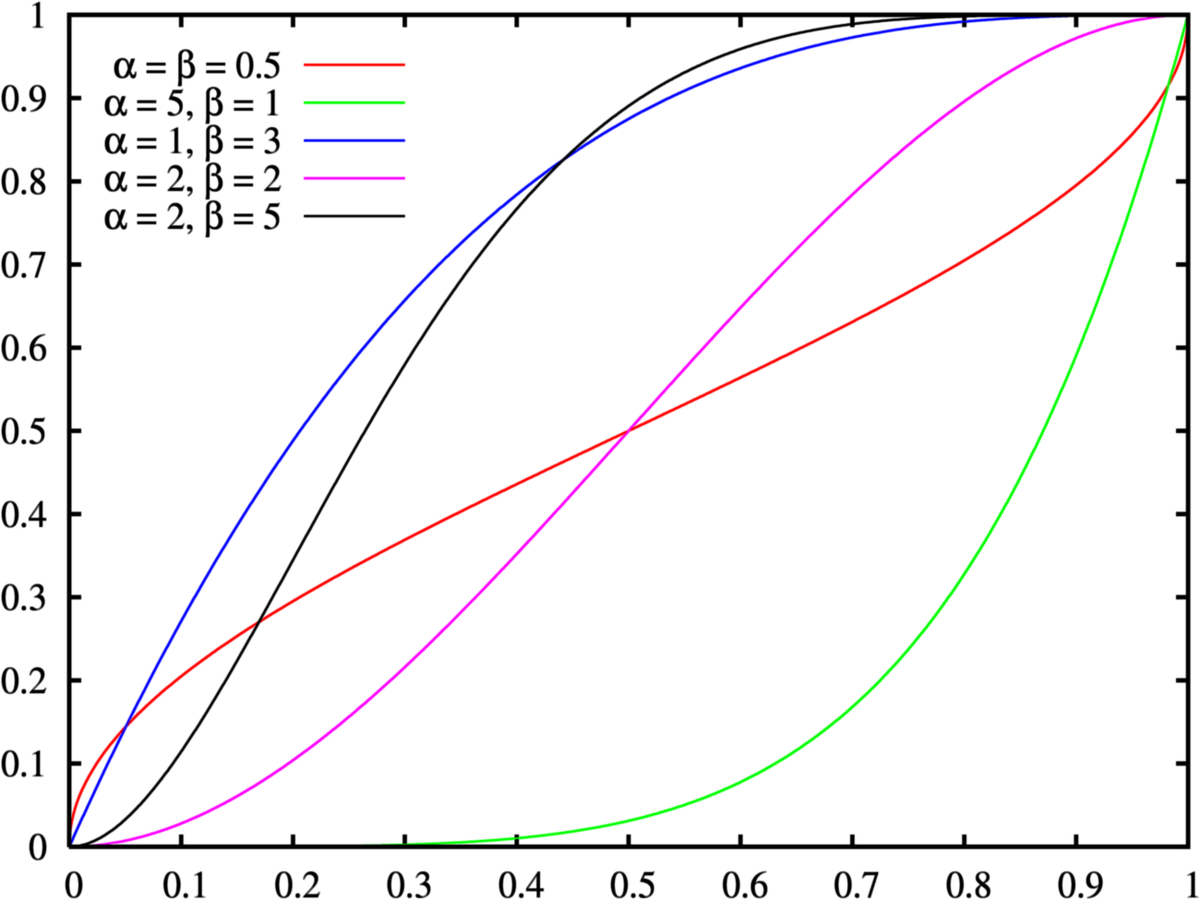
La fonction de répartition est
où Bx(α,β) est la fonction bêta incomplète et Ix(α,β) est la fonction bêta incomplète régularisée.
Estimation des paramètres
Soit la moyenne empirique
et
la variance. La méthode des moments fournit les estimations suivantes:
Propriétés
Moments
L'espérance et la variance d'une variable aléatoire bêta de paramètres α et β sont donnés par la formule:
L'asymétrie est
Le coefficient d'aplatissement (ou encore kurtosis) est:
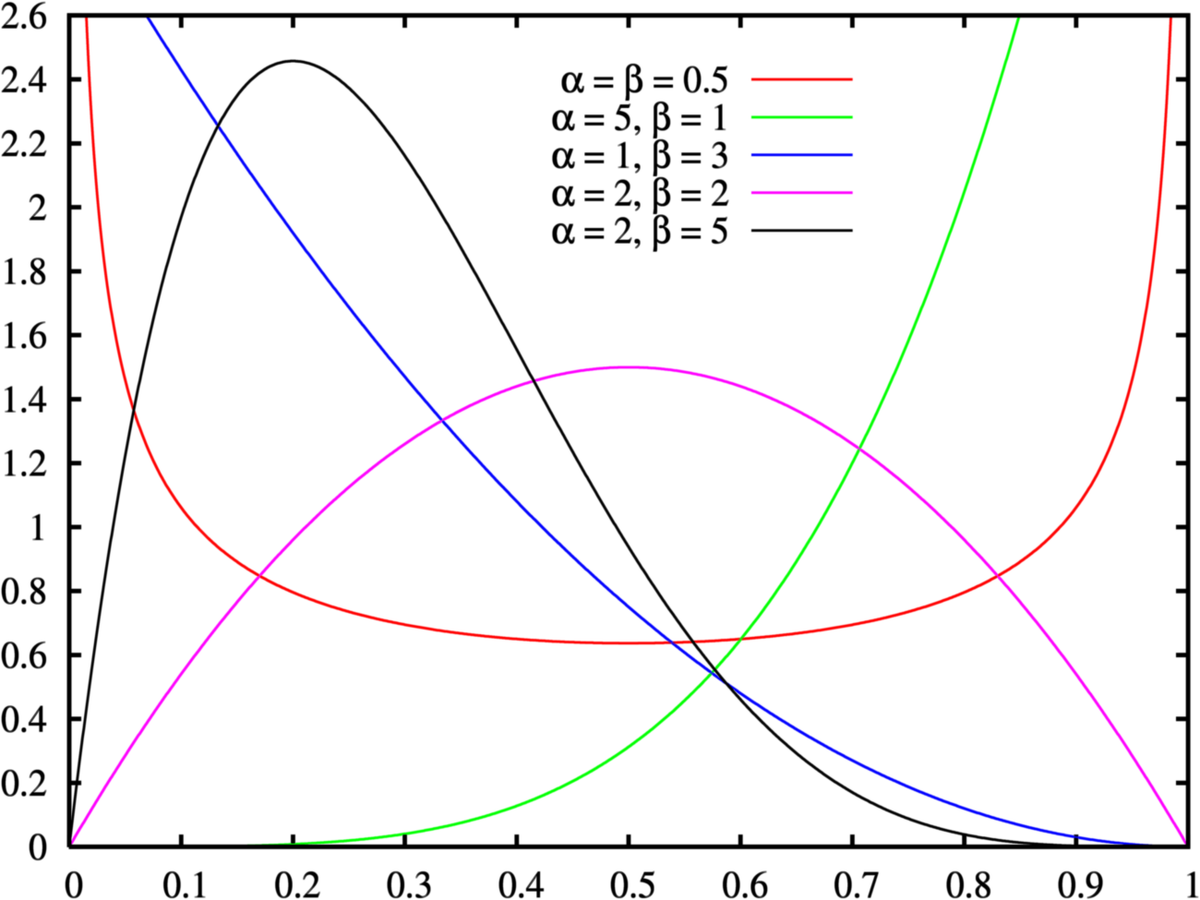
Formes
La densité de la loi bêta peut prendre différentes formes selon les valeurs des deux paramètres:
-
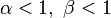
-
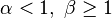
 est strictement décroissant (graphe bleu);
est strictement décroissant (graphe bleu);  est strictement convexe;
est strictement convexe;-
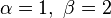
-
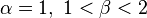
-
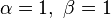
-
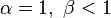
 est strictement croissant (graphe vert);
est strictement croissant (graphe vert);  est strictement convexe;
est strictement convexe;-
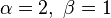
-
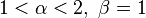
 est unimodal (graphes noir et violet).
est unimodal (graphes noir et violet).
Qui plus est, si α = β alors la densité est symétrique autour de 1/2 (graphes rouge et violet).
Distributions associées
- Si X a une distribution bêta, alors T=X/(1-X) est distribué selon la distribution bêta du second type;
- La loi Beta(1,1) est identique à la Loi uniforme continue;
- Si X et Y sont indépendamment distribués selon une loi Gamma, de paramètres (α, θ) et (β, θ) respectivement, alors X / (X + Y) est distribué selon une loi Beta(α,β);
- Si
![X \sim {\rm U}(0, 1]\,](https://static.techno-science.net/illustration/Definitions/autres/7/7487f663a469da4699b115cf58b4ce93_a2685a5882202977234ca447bad83036.png)
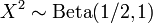
- La k-ème statistique d'ordre d'un n-échantillon de lois uniformes
![\ {\rm U}(0, 1]\,](https://static.techno-science.net/illustration/Definitions/autres/d/d61c50b7e4e5e2f7decf86b06e136929_7173bac4ebb63d403f82c32fd6f95376.png)
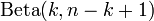
![x \in [0; 1]\!](https://static.techno-science.net/illustration/Definitions/autres/b/be450cd15463fbfc4e95de5eb88b6e90_b5dca9786fc3714f53708e0fcc277bf4.png)