Machine de Turing - Définition

Définition formelle

Plusieurs définitions formelles proches les unes des autres peuvent être données d'une machine de Turing. L'une d'elle, relativement courante, est choisie ici.

Une machine de Turing est un septuplet (Q,Γ,B,Σ,q₀,δ,F) où

• Q est un ensemble fini d'états ;
• Γ est l'alphabet de travail des symboles de la bande;
• est un symbole particulier (dit blanc) ;
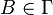
• Σ est l'alphabet des symboles en entrée ( ) ;
• est l'état initial ;
• est la fonction de transition ;
• est l'ensemble des états acceptants (ou finaux, terminaux).

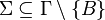
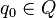
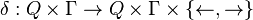
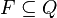
Les flèches dans la définition de δ représentent les deux déplacements possibles de la tête de lecture, à savoir le déplacement à gauche et le déplacement à droite. La signification de cette fonction de transition peut être expliquée sur l'exemple suivant : signifie que si la machine de Turing est dans l'état q₁ et qu'elle lit le symbole x, elle écrit y à la place de x, va dans l'état q₂, et déplace sa tête de lecture vers la gauche.

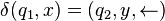
Le fonctionnement de la machine de Turing est alors le suivant. A chaque étape de son calcul, la machine évolue en fonction de l'état dans lequel elle se trouve, et du symbole inscrit dans la case du ruban où se trouve la tête de lecture. Ces deux informations permettent la mise à jour de l'état de la machine grâce à la fonction de transition. A l'instant initial, la machine se trouve dans l'état q₀, et le mot inscrit sur le ruban est l'entrée du programme. La machine s'arrête lorsqu'elle rentre dans un état terminal. Le résultat du calcul est alors le mot inscrit sur le ruban.

L'exemple suivant utilise une version très légèrement différente de machine de Turing dans laquelle une machine s'arrête si elle est dans un état terminal, et que le caractère écrit sur le ruban est le bon (ici le blanc).

Une machine de Turing réelle

Il est assez aisé de simuler une machine de Turing sur un ordinateur moderne, jusqu'au moment où la mémoire de l'ordinateur devient éventuellement pleine (si la machine de Turing utilise une très grande partie du ruban) !

Il est aussi possible de construire une machine de Turing purement mécanique. Le mathématicien Karl Scherer en construisit une en 1986 en utilisant des jeux de construction en métal et en plastique, et du bois. Sa machine, haute d'un mètre et demi utilise des ficelles pour lire, déplacer et écrire les données (représentées à l'aide de roulements à billes)^{[réf. souhaitée]}.

La machine est actuellement exposée dans le hall du département d'informatique de l'Université d'Heidelberg en Allemagne.

De même, en utilisant environ 300 miroirs, il est possible de créer une machine de Turing universelle optique en utilisant la méthode dite du fer à cheval conçue par Stephen Smale^{[réf. souhaitée]}.

Machines de Turing universelles

Toute machine de Turing calcule le résultat d'une fonction partielle sur des chaînes de caractères composées des caractères de son alphabet. En ce sens, une machine de Turing se comporte comme un ordinateur avec un programme déterminé.

Mais, comme Alan Turing le décrivit, on peut encoder la table d'actions d'une machine de Turing sous la forme d'une chaîne de caractères. On peut donc tenter de construire une machine de Turing qui suppose l'existence sur son ruban d'une chaîne de caractères encodant une table d'actions, suivie d'une chaîne de caractères constituant les données effectives du ruban, et calcule le contenu du ruban que la machine de Turing encodée aurait calculé.

Comme Alan Turing le montra dans son article fondateur, il est possible de créer une telle machine de Turing et puisqu'elle peut simuler le comportement de n'importe quelle autre machine de Turing, on l'appelle « machine de Turing universelle ».

Grâce à cet encodage des tables d'actions sous forme de chaînes de caractères, il devient en principe possible que les machines de Turing répondent à des questions à propos du comportement d'autres machines de Turing. Cependant, la plupart de ces questions sont indécidables, c'est-à-dire que la fonction en question ne peut pas être calculée par une machine de Turing.
Par exemple, la question de savoir si une machine de Turing atteint à un moment donné un état d'arrêt ou ne l'atteint jamais pour une entrée particulière, ou pour toutes les entrées possibles, connue sous le nom de problème de l'arrêt, fut démontré comme étant indécidable par Turing. Le théorème de Rice montre que toute propriété non triviale sur le langage acceptée par une machine de Turing est indécidable.

Si on élargit la définition pour y inclure les machines de Turing qui simulent des modèles de calcul Turing-complets, et non plus seulement les machines de Turing qui simulent directement d'autres machines de Turing, une machine de Turing universelle peut être relativement simple, et utiliser seulement quelques états et symboles. Par exemple, il existe une machine de Turing universelle de taille 2×18 (c'est-à-dire 2 états, et 18 symboles).
Les plus petites machines de Turing universelles connues ont les tailles suivantes : 2×18, 3×10, 4×6, 5×5, 7×4, 10×3, 22×2. Ces dernières simulent un modèle appelé tag system.

Une machine de Turing de taille 2×3 proposée par Stephen Wolfram, a été annoncée comme la plus petite machine de Turing universelle. La preuve est due à Alex Smith. Cependant la notion d'universalité utilisée dans cette preuve n'est pas la même que celle décrite informellement ci-dessus. En particulier, elle nécessite d'écrire une infinité de symboles initialement sur le ruban pour préparer le calcul.

Une machine de Turing universelle est Turing-complète. Elle peut calculer toute fonction récursive, analyser tout langage récursif, et accepter tout langage partiellement décidable. Selon la thèse de Church-Turing, les problèmes résolubles par une machine de Turing universelle sont exactement les problèmes résolubles par un algorithme ou par une méthode concrète de calcul, en supposant une définition raisonnable de ces termes.