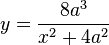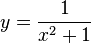Maria Gaetana Agnesi - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

Margarita Gaetana Angiolo Maria Agnesi (née le 16 mai 1718 à Milan et morte le 9 janvier 1799 dans la même ville) était une linguiste, mathématicienne et philosophe italienne. On attribue à Agnesi le premier livre traitant à la fois de calcul différentiel et de calcul intégral. Elle était un membre honorifique de la faculté de l'Université de Bologne.
Biographie
Son père, Pietro, était un riche négociant en drap. Enfant prodige, elle parlait le français et l’italien à l’âge de cinq ans. À neuf ans, elle lit un discours en latin d’une heure à une réunion d’universitaires, où elle aborde le droit des femmes a recevoir une éducation. À treize ans, elle maîtrisait en outre le grec, l’hébreu, l’espagnol, l’allemand, le latin et probablement d’autres langues. Ses talents de polyglotte lui valaient l’admiration de ses proches. Elle s’occupe également de l’éducation de ses jeunes frères. À quinze ans, son père commence à l’inviter à son cercle d’intellectuels bolognais qui se réunissent chez lui. Agnesi y présente régulièrement des exposés sur les sujets philosophiques les plus complexes. Elle fait paraître en 1738 un recueil de ceux-ci dans ses Propositiones Philosophicae, série de 191 essais sur la philosophie et l’histoire naturelle. On possède des descriptions de ces rencontres grâces aux Lettres historiques et critiques sur l'Italie Charles de Brosses (1709-1777). Il semble que la jeune Maria n’appréciait pas ces démonstrations publiques, qui s’interrompent vers sa vingtième année. Elle envisage alors d’entrer au couvent. C’est le père Ramiro Rampinelli (1697-1759) qui l’initie aux mathématiques lors de ses visites à la maison paternelle. C’est avec son aide qu’elle étudie l’Analyse démontrée (1708) de Charles René Reyneau (1656-1728).
Ses Instituzioni analitiche ad uso della gioventu italiana, de 1748, sont dédiées à Marie-Thérèse d’Autriche (1717-1780). Le premier volume traite de l’analyse des quantités finies et le second de l’analyse des infinitésimaux. Le second volume est traduit en français par Pierre Thomas Antelmy (1730-1783) avec des ajouts de Charles Bossut (1730-1814) en 1775. La traduction en anglais est assurée par John Colson (1680-1760), le détenteur de la chaire lucasienne de Cambridge. Pour connaître la valeur de son travail, elle soumet la première partie à divers mathématiciens de sa ville notamment Jacopo Riccati (1676-1754). Son premier volume lui vaut une notoriété certaine, un rapport présenté à l’Académie des sciences de Paris par Étienne Mignot de Montigny (1714-1782) lui déclare :
« Permettez-moi, mademoiselle, de joindre mon hommage personnel aux applaudissements de l’Académie. J’ai eu le plaisir de faire connaître à mon pays un ouvrage extrêmement utile et longtemps désiré, et qui jusqu’à présent, en France et en Angleterre, n’existait qu’à l’état de projet. Je n’ai connaissance d’aucun ouvrage de ce type qui soit plus clair, plus méthodique, plus complet que vos Institutions analytiques. Il n’existe aucun livre en aucune langue qui puisse guider plus sûrement, plus rapidement et conduire plus loin ceux qui veulent s’avancer dans la connaissance des sciences mathématiques. J’admire particulièrement l’art avec lequel vous présentez dans une méthode uniforme les diverses conclusions dispersées dans l’œuvre de plusieurs géomètres, et atteintes avec des méthodes extrêmement différentes. »
Maria Agnesi écrit un commentaire sur le Traité analytique des sections coniques du marquis de L'Hôpital mais qui ne sera jamais publié. Elle évoque la courbe connue sous le nom de la sorcière d'Agnesi ou versiera comme elle la nomme en 1748. Des exemples de cette courbe peuvent être donnés par l’équation :
où a est n’importe quelle constante non nulle ; l’équation :
étant la forme la plus simple. Cette courbe avait été auparavant étudiée par Pierre de Fermat (1601-1665) et Guido Grandi (1671-1742) en 1703.

Le pape Benoît XIV lui écrit alors pour lui dire qu’il avait étudié les mathématiques dans sa jeunesse et qu’il voyait bien ce que son œuvre pouvait apporter à la reconnaissance de l’Italie et de l’Académie de Bologne ; il nomme peu après Agnesi comme lecteur honoraire à l’université de Bologne. À la suite de cela, le président de cette Académie et trois professeurs de l’université lui proposent la chaire de mathématiques. Une lettre du pape du 26 septembre 1750 souligne que ce sont ses seuls mérites qui lui donnent droit à cette chaire et qu’elle n’a pas à les remercier de la lui proposer. En octobre, Agnesi reçoit la confirmation du pape de son engagement, mais elle préfère se consacrer à la dévotion et se retire de la vie publique. Bien que son nom demeure durant quarante-cinq ans dans les registres de l’université, Agnesi n’est jamais venu à Bologne. Après la mort de son père en 1752, elle se consacre entièrement aux pauvres.