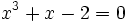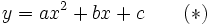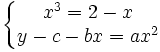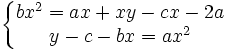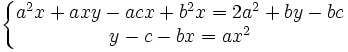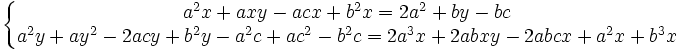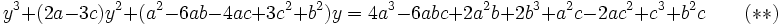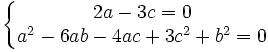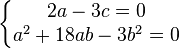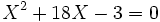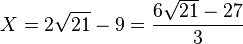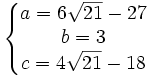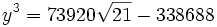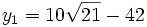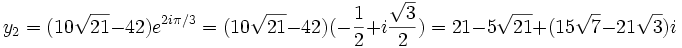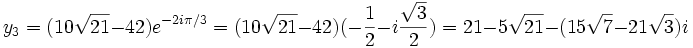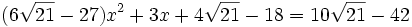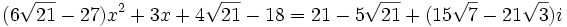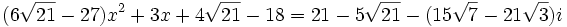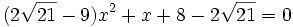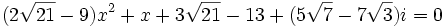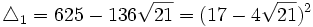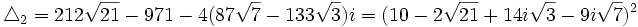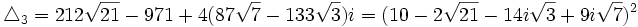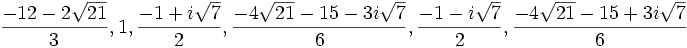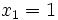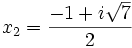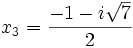Méthode de Tschirnhaus - Définition

Application à la résolution des équations cubiques

Nous allons exposer la méthode sur l'exemple suivant :

Posons :

Les deux équations précédentes se mettent sous la forme :

Nous devons éliminer x entre ces deux équations. Pour cela, nous remplaçons la première équation par le produit membre à membre de ces deux équations. Après simplification, nous obtenons :

Cette façon de procéder permet de diminuer le degré de l'une des équations par rapport à x. Nous allons donc réitérer le processus jusqu'à ce que x ait disparu de l'une des équations. D'autre part, comme nous faisons des produits membre à membre, nous risquons d'introduire des solutions parasites. Il nous sera donc nécessaire à la fin de la résolution de vérifier que toutes les solutions trouvées vérifient bien l'équation à résoudre.

Après un nouveau produit membre à membre, nous obtenons :

Après un nouveau produit membre à membre en remplaçant cette fois la deuxième équation, nous obtenons :

Un dernier produit membre à membre nous donne après réduction des termes semblables et simplification par a²x :

Nous devons maintenant déterminer a, b, c de façon à ce que :

En tirant c de la première équation et en reportant dans la deuxième équation, nous obtenons :

Nous voyons alors que le rapport a/b est racine de l'équation :

L'une des racines de cette équation étant :

On peut en déduire pour a, b, c le choix des valeurs suivantes :

En reportant ces valeurs d'une part dans (*), on obtient :

Et d'autre part dans (**), on obtient :

D’où l'on déduit les trois valeurs possibles de y :

Il nous suffit de reporter ces trois valeurs de y dans (***) pour obtenir successivement les trois équations du second degré suivantes :

Qui se simplifient sous la forme :

Il ne nous reste plus qu'à résoudre ces trois équations pour en déduire les valeurs possibles de x. Les trois discriminants de ces équations du second degré sont respectivement :

On en déduit respectivement les six valeurs possibles pour x :

Comme nous avons fait des produits membre à membre au début, nous risquons d'avoir introduit des racines parasites. Nous devons donc vérifier que les valeurs obtenues pour x vérifient bien l'équation à résoudre. Nous constatons que seulement trois des six valeurs obtenues sont bien solution de l'équation. Ces valeurs sont :

Remarque historique

Cette méthode est la première méthode générale de résolution des équations à avoir été publiée. Sa publication remonte à 1683.

Equation du cinquième degré

Voir à ce propos l'article Radical de Bring.

Autres méthodes de résolution d'équations

• Méthode de Bézout
• Méthode de Cardan
• Méthode de Sotta
• Méthode de Ferrari
• Méthode de Descartes
• Méthode d'Hermite

v · d · m Méthodes de résolution d'équations
Résolution d'équations polynomiales	Méthode de Bézout · Méthode de Cardan · Méthode de Sotta · Méthode de Ferrari · Méthode de Descartes · Méthode de Tschirnhaus · Méthode d'Hermite
Recherche d'un zéro	Méthode de dichotomie · Méthode de Newton · Méthode de la sécante · Méthode de Müller · Méthode de Brent · Méthode de la fausse position · Méthode de Héron · Méthode de Laguerre · Méthode du cercle de séparation · Méthode de Halley · Méthode de Householder . Méthode de Quasi-Newton