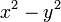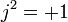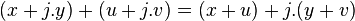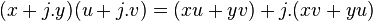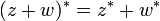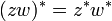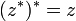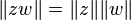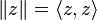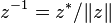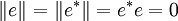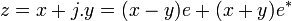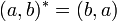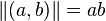Nombre complexe fendu - Définition

Introduction

En mathématiques, les nombres complexes fendus sont une extension des nombres réels définis de manière analogue aux nombres complexes (usuels). La différence-clef entre les deux est que la multiplication des nombres complexes (usuels) respecte la norme euclidienne standard (carrée) :

sur

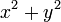
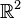
alors que la multiplication des nombres complexes fendus, quant à elle, respecte la norme de Minkowski ou norme lorentzienne (carrée)

Les nombres complexes fendus ont beaucoup d'autres noms, voir la section des synonymes ci-dessous.

Un espace vectoriel réel à deux dimensions muni du produit interne de Minkowski est appelé un espace de Minkowski de dimension 1+1, souvent noté . Tout comme la géométrie euclidienne du plan euclidien peut être décrite avec les nombres complexes, la géométrie lorentzienne du plan de Minkowski peut être décrite avec les nombres complexes fendus.

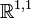
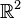
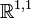
Le nom fendu provient du fait que les signatures de la forme (p,p) sont appelées signatures fendues. En d'autre mots, les nombres complexes fendus sont similaires aux nombres complexes mais dans la signature fendue (1,1).

Définition

Un nombre complexe fendu est de la forme :

où x et y sont des nombres réels et la quantité j définie par (voir les Tessarines) :

L'ensemble de tous ces z est appelé le plan complexe fendu. L'addition et la multiplication des nombres complexes fendus sont définies par

Cette multiplication est commutative, associative et distributive sur l'addition.

Conjugué, norme, et produit interne

Comme pour les nombres complexes, on peut définir la notion de conjugué complexe fendu. Si

,

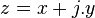
le conjugué de z est défini par

.

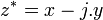
Le conjugué satisfait les propriétés similaires du conjugué complexe usuel :

Ces trois propriétés impliquent que le conjugué complexe fendu est un automorphisme d'ordre 2.

La norme carrée (ou forme quadratique) d'un nombre complexe fendu est donnée par

.

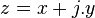
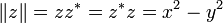
Cette norme n'est pas définie positivement mais possède plutôt une métrique (1,1). Une propriété importante de cette norme est qu'elle est préservée par la multiplication complexe fendue :

Le produit interne associé (1,1) est donné par

où et et

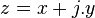
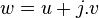
Les nombres complexes fendus z et w sont dits orthogonaux hyperboliques si <z, w> = 0.

Un nombre complexe fendu est inversible si et seulement si sa norme est différente de zéro ( ). L'inverse d'un tel élément est donné par

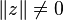
Les nombres complexes fendus qui ne sont pas inversibles sont appelés éléments nuls. Ceux-ci sont tous de la forme pour un certain nombre réel a.

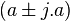
La base diagonale

Il existe deux éléments idempotents non-triviaux donnés par et (c'est-à-dire que et ). Ces deux éléments sont nuls :

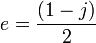
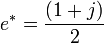
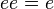
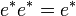
Il est souvent commode d'utiliser e et e^* comme une base alternative pour le plan complexe fendu. Cette base est appelée la base diagonale ou base nulle. Le nombre complexe fendu z peut être écrit dans la base nulle sous la forme

Si nous notons le nombre

pour les nombres réels a et b par (a,b) alors la multiplication complexe fendue est donnée par

.

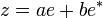
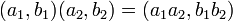
Dans cette base, il devient clair que les nombres complexes fendus sont isomorphes à la somme directe avec l'addition et la multiplication définie ci-dessus.

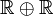
Le conjugué complexe fendu dans la base diagonale est donné par

et la norme par